Structure of Periodic Table
Early Attempts at Organization
The quest to understand the fundamental building blocks of matter and their relationships has been a driving force in scientific inquiry for centuries. Before the modern understanding of atomic structure and the elegant organization of the periodic table, early chemists and natural philosophers grappled with the ever-growing number of discovered elements. Driven by a desire to impose order on this seemingly disparate collection of substances, they made pioneering attempts to classify and organize the elements based on their observed properties and, later, their atomic weights. These initial forays, though ultimately incomplete and sometimes flawed, were crucial stepping stones in the development of our modern understanding of the elements and their periodic behavior. Two particularly notable and influential examples of these early organizational efforts are Johann Wolfgang Döbereiner's Triads and John Newlands' Law of Octaves.
The Murky Landscape of Early Chemistry:
To appreciate the significance of Döbereiner and Newlands' contributions, it's essential to understand the state of chemistry in the late 18th and early to mid-19th centuries. While the concept of an "element" had been gaining traction since the time of Robert Boyle, the distinction between elements, compounds, and mixtures was not always clear-cut. The number of known elements was steadily increasing, thanks to advancements in experimental techniques and the isolation of new substances. However, there was no unifying theoretical framework to explain their diverse properties and behaviors.
Early attempts at classification often relied on superficial similarities, such as physical state (solid, liquid, gas) or general chemical behavior (metals vs. non-metals). While these categories provided a basic level of grouping, they lacked the predictive power and deeper insight that chemists sought. The emerging field of quantitative chemistry, with its focus on precise measurements of mass and composition, began to reveal underlying relationships that hinted at a more fundamental order. The concept of atomic weight, though still under development and subject to some inaccuracies, was becoming increasingly important.
Johann Wolfgang Döbereiner and the Law of Triads (Early 19th Century):
Johann Wolfgang Döbereiner (1780-1849), a German chemist, was among the first to recognize patterns in the properties of certain groups of elements. In the 1810s and 1820s, he observed that elements with similar chemical properties often occurred in groups of three, which he termed "triads." The most striking feature of these triads was the apparent mathematical relationship between their atomic weights.
Döbereiner noticed that when he arranged the elements within a triad in order of increasing atomic weight, the atomic weight of the middle element was approximately the average of the atomic weights of the other two. Furthermore, the properties of the middle element were often intermediate between the properties of the other two.
Some of Döbereiner's most prominent triads included:
-
Lithium (Li), Sodium (Na), Potassium (K): These alkali metals share striking similarities in their chemical reactivity. They react vigorously with water to form strong alkaline solutions, they readily lose one electron to form +1 ions, and they form similar compounds. The atomic weights at the time were approximately 7, 23, and 39. The average of the atomic weights of lithium and potassium is (7 + 39) / 2 = 23, which is very close to the atomic weight of sodium.
-
Calcium (Ca), Strontium (Sr), Barium (Ba): This group of alkaline earth metals also exhibits similar properties. They react with water (though less vigorously than alkali metals), they lose two electrons to form +2 ions, and their compounds share similar characteristics. The atomic weights were roughly 40, 88, and 137. The average of calcium and barium is (40 + 137) / 2 = 88.5, again close to the atomic weight of strontium.
-
Chlorine (Cl), Bromine (Br), Iodine (I): These halogens are all reactive non-metals that exist as diatomic molecules. They share similar reactions with metals, forming salts. Their atomic weights were approximately 35.5, 80, and 127. The average of chlorine and iodine is (35.5 + 127) / 2 = 81.25, close to the atomic weight of bromine.
Döbereiner identified several other potential triads, such as sulfur, selenium, and tellurium, though the agreement in atomic weights was not always as precise.
Significance of Döbereiner's Triads:
Döbereiner's work was significant for several reasons:
- First Recognition of Systematic Relationships: It was one of the earliest demonstrations of a systematic relationship between the properties of elements and their atomic weights. This was a crucial step towards understanding an underlying order in the chemical world.
- Stimulated Further Research: Döbereiner's observations sparked interest among other chemists and encouraged them to look for similar patterns and relationships. It demonstrated that the properties of elements were not random but might be governed by some underlying principle.
- Foundation for Future Classification: Although the concept of triads was limited, it provided a foundation upon which later scientists could build more comprehensive classification systems. It highlighted the importance of considering groups of elements with similar properties.
Limitations of Döbereiner's Triads:
Despite its significance, Döbereiner's concept of triads had several limitations:
- Limited Applicability: The triad system was only applicable to a small number of known elements. Many elements could not be easily grouped into triads with consistent relationships in atomic weights and properties.
- Lack of a Theoretical Basis: Döbereiner's observations were empirical, meaning they were based on experimental data rather than a fundamental theoretical understanding. He could observe the patterns but could not explain why they occurred. The nature of atoms and the reason for the relationship between atomic weight and properties remained a mystery.
- Ambiguity in Some Cases: In some potential triads, the agreement in atomic weights was not as clear-cut, leading to some ambiguity in the classification.
Despite these limitations, Döbereiner's work was a valuable contribution to the early attempts at organizing the elements. It demonstrated that there was an underlying order waiting to be discovered and paved the way for more comprehensive systems.
John Newlands and the Law of Octaves (Mid-19th Century):
By the mid-19th century, the number of known elements had significantly increased, and more accurate atomic weights were being determined. Building upon the foundation laid by earlier chemists, including Döbereiner, John Alexander Reina Newlands (1837-1898), an English chemist, made another significant attempt to organize the elements.
In 1865, Newlands presented his "Law of Octaves." He arranged the known elements in order of increasing atomic weight and observed that after every seven elements, the eighth element had properties similar to the first, the ninth similar to the second, and so on. He drew an analogy to the musical scale, where after seven notes, the eighth note is an octave higher and shares a similar musical quality with the first.
Newlands' arrangement looked something like this (using simplified atomic weight values for illustration):
| Number | Element | Atomic Weight | Properties |
|---|---|---|---|
| 1 | Hydrogen (H) | 1 | Gas, highly reactive |
| 2 | Lithium (Li) | 7 | Soft metal, reacts with water |
| 3 | Beryllium (Be) | 9 | Light metal, amphoteric oxide |
| 4 | Boron (B) | 11 | Metalloid, forms acidic oxides |
| 5 | Carbon (C) | 12 | Non-metal, forms many compounds |
| 6 | Nitrogen (N) | 14 | Gas, relatively unreactive |
| 7 | Oxygen (O) | 16 | Gas, highly reactive |
| 8 | Fluorine (F) | 19 | Gas, highly reactive halogen |
| 9 | Sodium (Na) | 23 | Soft metal, reacts with water (similar to Li) |
| 10 | Magnesium (Mg) | 24 | Light metal, forms basic oxide (similar to Be) |
| 11 | Aluminum (Al) | 27 | Metal, amphoteric oxide (similar to B) |
| 12 | Silicon (Si) | 28 | Metalloid, forms network covalent structures (similar to C) |
| 13 | Phosphorus (P) | 31 | Non-metal, forms acidic oxides (similar to N) |
| 14 | Sulfur (S) | 32 | Non-metal, forms various oxides (similar to O) |
| 15 | Chlorine (Cl) | 35.5 | Reactive halogen (similar to F) |
| ... | ... | ... | ... |
Significance of Newlands' Law of Octaves:
Newlands' work was a significant step forward from Döbereiner's triads:
- More Comprehensive Organization: Unlike Döbereiner, Newlands attempted to organize all the known elements into a single system, rather than focusing on small groups.
- Explicit Recognition of Periodicity: Newlands was the first to explicitly recognize the idea of periodicity – the recurrence of similar properties at regular intervals when elements are arranged in order of increasing atomic weight. This was a crucial insight that would later form the basis of the modern periodic table.
- Stimulated Debate and Further Investigation: While initially met with skepticism, Newlands' work stimulated debate and further investigation into the relationships between elements and their atomic weights.
Reception and Limitations of Newlands' Law of Octaves:
Despite its significance, Newlands' Law of Octaves was initially met with ridicule and skepticism by the scientific community. He famously presented his paper to the Chemical Society of London in 1866, where he was met with disbelief and even sarcasm. One member reportedly asked him if he had tried arranging the elements alphabetically.
The reasons for the negative reception were several:
- Forced Fit: Newlands' law worked reasonably well for the lighter elements up to calcium. However, beyond calcium, the pattern began to break down, and he had to force elements with dissimilar properties into the same groups to maintain the octaves.
- Lack of Space for Undiscovered Elements: Newlands' system did not provide any gaps or placeholders for undiscovered elements. This was a significant flaw, as chemists were aware that more elements likely existed.
- Inclusion of Transition Metals: The transition metals, with their variable valencies and complex properties, did not fit neatly into Newlands' octave arrangement.
- Skepticism Towards the Musical Analogy: The analogy to musical octaves was seen as frivolous and lacking scientific rigor by some chemists.
Despite the initial negative reaction, Newlands continued to defend his work. It is now recognized that his Law of Octaves contained a fundamental truth about the periodic nature of the elements, even though his system was ultimately flawed.
The Legacy of Döbereiner and Newlands:
While neither Döbereiner's triads nor Newlands' Law of Octaves ultimately provided a perfect or universally accepted system for organizing the elements, their contributions were crucial in the historical development of the periodic table.
- Demonstrating Underlying Order: Both scientists demonstrated that there was an underlying order and relationship among the elements, suggesting that their properties were not random.
- Highlighting the Importance of Atomic Weight: Their work emphasized the significance of atomic weight as a key parameter in understanding and classifying elements.
- Paving the Way for Mendeleev: The insights gained from their attempts directly influenced Dmitri Mendeleev, who, building upon their work and incorporating new data, developed the first widely accepted and predictive periodic table in 1869. Mendeleev acknowledged the contributions of his predecessors, including Döbereiner and Newlands.
In conclusion, Döbereiner's Triads and Newlands' Law of Octaves represent important early attempts to bring order to the growing number of known elements. While limited in their scope and accuracy, they were pioneering efforts that demonstrated the existence of systematic relationships between elemental properties and atomic weights. These early attempts, though imperfect, served as crucial stepping stones in the long and fascinating journey towards our modern understanding of the periodic table and the fundamental nature of matter. They exemplify the iterative nature of scientific progress, where early ideas, even with their flaws, can lay the foundation for groundbreaking discoveries.
Mendeleev's Periodic Law and His Periodic Table
Dmitri Ivanovich Mendeleev, a brilliant Russian chemist, is celebrated as one of the most influential figures in the history of chemistry. His groundbreaking work in the mid-19th century led to the formulation of the Periodic Law and the creation of the first widely accepted Periodic Table of Elements. This system, based on the atomic weights of elements and their recurring chemical properties, revolutionized the understanding of the fundamental building blocks of matter and laid the groundwork for the modern periodic table we use today. Mendeleev's genius lay not only in his insightful observations but also in his bold predictions, which were later confirmed, solidifying the significance and validity of his work.
The Genesis of the Periodic Law:
Mendeleev's journey towards the Periodic Law was a culmination of his meticulous study of chemical properties and atomic weights. He spent considerable time compiling and analyzing the known properties of elements, focusing on their combining capacities (valency) and their interactions with oxygen and hydrogen. Legend has it that Mendeleev, while struggling to organize the elements, envisioned the arrangement in a dream. While the truth of this anecdote is debatable, it underscores the intensive and dedicated effort he poured into his work.
In 1869, Mendeleev published his first version of the periodic table. His central insight, which became the cornerstone of his Periodic Law, can be stated as follows:
"The properties of the elements are a periodic function of their atomic weights."
This seemingly simple statement held profound implications. It meant that if elements were arranged in order of increasing atomic weight, elements with similar chemical properties would appear at regular intervals. This periodicity was the key to unlocking a deeper understanding of the relationships between elements.
Mendeleev's Periodic Table (1869):
Mendeleev's periodic table was a bold departure from previous attempts at classification. It was organized into groups (vertical columns) and series (horizontal rows). Elements within the same group exhibited similar chemical properties, while those in the same series showed a gradual change in properties.
The structure of Mendeleev's table was not without its nuances and departures from a strictly increasing order of atomic weights. Crucially, Mendeleev recognized that to maintain elements with similar properties in the same group, he sometimes had to place elements out of strict atomic weight order. This bold move demonstrated his conviction in the periodicity of properties as the guiding principle.
Here is a representation of a simplified version of Mendeleev's 1869 periodic table (keeping in mind the limitations of text-based representation):
| Group I | Group II | Group III | Group IV | Group V | Group VI | Group VII | Group VIII |
|---|---|---|---|---|---|---|---|
| H = 1 | |||||||
| Li = 7 | Be = 9.4 | B = 11 | C = 12 | N = 14 | O = 16 | F = 19 | |
| Na = 23 | Mg = 24 | Al = 27.3 | Si = 28 | P = 31 | S = 32 | Cl = 35.5 | |
| K = 39 | Ca = 40 | - = 44 | Ti = 48 | V = 51 | Cr = 52 | Mn = 55 | Fe = 56, Co = 59, Ni = 59 |
| (Cu = 63) | Zn = 65 | - = 68 | - = 72 | As = 75 | Se = 78 | Br = 80 | |
| Rb = 85 | Sr = 87.5 | Yt = 88 | Zr = 90 | Nb = 94 | Mo = 96 | - = 100 | Ru = 104, Rh = 104, Pd = 106 |
| (Ag = 108) | Cd = 112 | In = 113 | Sn = 118 | Sb = 122 | Te = 128 | I = 127 | |
| Cs = 133 | Ba = 137 | Di = 138 | Ce = 140 | ||||
| - = 178 | Ta = 182 | W = 184 | Os = 195, Ir = 197, Pt = 198 | ||||
| (Au = 199) | Hg = 200 | Tl = 204 | Pb = 207 | Bi = 208 | |||
| Th = 231 | U = 240 |
Key Observations and Features of Mendeleev's Table:
- Arrangement by Atomic Weight: The primary organizing principle was the increasing atomic weight of the elements.
- Grouping by Similar Properties: Elements within the same vertical group exhibited similar chemical behaviors. For instance, Group I contained the alkali metals (Li, Na, K), known for their high reactivity with water. Group VII housed the halogens (F, Cl, Br, I), which are highly reactive nonmetals.
- Leaving Gaps for Undiscovered Elements: This was arguably Mendeleev's most audacious and significant contribution. He noticed that to maintain the periodicity of properties, there were gaps in his table. Instead of forcing known elements into these spaces, he boldly predicted the existence of yet-undiscovered elements that would fill these gaps. He even went so far as to predict the properties of these missing elements based on the properties of their neighboring elements.
- Correction of Atomic Weights: In some instances, Mendeleev questioned the accepted atomic weights of certain elements. By considering their position in the periodic table and their properties, he suggested revisions to these weights, some of which were later proven to be correct.
- Placement of Transition Metals: Mendeleev recognized the unique behavior of the transition metals and placed them in separate groups or within Group VIII, acknowledging their characteristic variable valencies and catalytic properties.
The Power of Prediction: Mendeleev's Triumph:
Mendeleev's predictions were not mere guesses; they were based on the logical framework of his periodic law. He predicted the properties of three elements in particular detail:
- Eka-boron (Eb): Predicted to lie below aluminum in Group III. In 1879, Lars Fredrik Nilson discovered scandium (Sc), whose properties closely matched Mendeleev's predictions for eka-boron.
- Eka-aluminum (Ea): Predicted to lie below aluminum in Group III. In 1875, Paul-Émile Lecoq de Boisbaudran discovered gallium (Ga), and its properties were remarkably similar to those predicted for eka-aluminum.
- Eka-silicon (Es): Predicted to lie below silicon in Group IV. In 1886, Clemens Winkler discovered germanium (Ge), and once again, its properties aligned remarkably well with Mendeleev's predictions for eka-silicon.
The discovery of these elements with properties matching Mendeleev's predictions was a monumental validation of his periodic law and his periodic table. It solidified his place as a visionary scientist and elevated the periodic table to a fundamental principle of chemistry.
Significance and Impact of Mendeleev's Work:
Mendeleev's periodic table had a profound and lasting impact on the field of chemistry:
- Organization of Chemical Knowledge: It provided a systematic framework for organizing the vast amount of chemical information known at the time. It highlighted relationships between elements that were not previously apparent.
- Predictive Power: The ability to predict the existence and properties of undiscovered elements was revolutionary. It guided experimental research and accelerated the discovery of new elements.
- Foundation for Atomic Theory: Although Mendeleev's table was based on atomic weights, it paved the way for a deeper understanding of atomic structure. The periodic law hinted at an underlying order within the atom that was later explained by the discovery of protons, neutrons, and electrons.
- Understanding Chemical Bonding and Reactivity: The periodic table provided insights into the valency and chemical reactivity of elements, helping to explain how elements combine to form compounds.
- Development of New Materials: The periodic table continues to be a valuable tool in the search for and development of new materials with specific properties.
Limitations of Mendeleev's Table:
Despite its groundbreaking nature, Mendeleev's periodic table had certain limitations:
- Anomalies in Atomic Weight Order: As mentioned earlier, to maintain elements with similar properties in the same group, Mendeleev had to place some elements out of strict increasing atomic weight order (e.g., Tellurium (Te) before Iodine (I)). This suggested that atomic weight was not the sole determining factor in the periodic properties.
- Placement of Hydrogen: Hydrogen, with its unique properties, was difficult to place definitively within a single group.
- Lack of Explanation for Periodicity: Mendeleev's table described the periodicity of properties but did not explain the underlying cause of this periodicity.
- Discovery of Noble Gases: The noble gases (Helium, Neon, Argon, etc.) were discovered after Mendeleev's initial work. Their inert nature and full outer electron shells did not easily fit into the existing groups of his table. He later accommodated them by adding a new Group VIII (or sometimes referred to as Group 0).
- Isotopes: The discovery of isotopes (atoms of the same element with different atomic weights) presented a challenge to the atomic weight-based organization. Isotopes of the same element would have different positions in Mendeleev's table, despite having the same chemical properties.
Modern Periodic Law and Moseley's Experiment Explained
Element Properties Calculator
The Modern Periodic Law states that the physical and chemical properties of the elements are periodic functions of their atomic numbers. This means that when elements are arranged in order of increasing atomic number, elements with similar properties occur at regular intervals.
This is a crucial update to the older Periodic Law, which arranged elements by increasing atomic mass. While the older law worked for many elements, it ran into inconsistencies and anomalies, such as the placement of tellurium (Te) before iodine (I) despite Te having a slightly higher atomic mass.
Key Concept: Atomic Number
The atomic number (Z) of an element is defined as the number of protons in the nucleus of an atom of that element. It is a fundamental property of an element and uniquely identifies it.
Moseley's Experiment: Unveiling the Importance of Atomic Number
Henry Gwyn Jeffreys Moseley, a British physicist, conducted a groundbreaking series of experiments in the early 20th century (around 1913-1914) that provided strong experimental evidence for the significance of atomic number and ultimately led to the formulation of the Modern Periodic Law.
The Experiment:
Moseley used an X-ray tube to bombard various elements with high-energy electrons. When these electrons struck the atoms of the target element, they would knock out inner-shell electrons. As other electrons transitioned to fill these vacancies, they would emit characteristic X-rays, meaning X-rays with specific frequencies unique to the element.
Here's a simplified breakdown of the experimental setup:
- X-ray tube: A vacuum tube where electrons are accelerated towards a target.
- Target (Anode): Different elements were used as the target material.
- Electron Beam: A stream of high-energy electrons.
- Characteristic X-rays: The X-rays emitted by the target element.
- Measurement of X-ray Frequencies: Moseley used techniques to measure the frequencies () of the emitted X-rays.
Moseley's Observations and Mathematical Relationship:
Moseley systematically studied the characteristic X-ray frequencies emitted by different elements. He observed a consistent pattern:
-
As the atomic mass of the target element increased, the frequency of the emitted X-rays also generally increased. This was somewhat expected based on previous knowledge.
-
Crucially, Moseley found a more precise and fundamental relationship between the frequency of the X-rays and the position of the element in the periodic table. He realized that the order of the elements in terms of their X-ray frequencies matched the order predicted by increasing atomic number, even where atomic masses had created inconsistencies.
Moseley formulated a mathematical relationship that elegantly described his findings:
Where:
- represents the frequency of the emitted X-ray.
- is the atomic number of the target element.
- is a proportionality constant that depends on the series of spectral lines being observed (e.g., K-alpha, L-alpha).
- is a small correction factor, often referred to as the screening constant, which accounts for the shielding effect of inner electrons on the outer electrons involved in the X-ray emission.
Interpretation of the Mathematical Relationship:
This equation clearly demonstrates a direct linear relationship between the square root of the X-ray frequency () and the atomic number (). This was a revolutionary finding because it showed that the atomic number, the number of protons in the nucleus, was the fundamental property determining the characteristic X-ray frequencies and, by extension, the underlying structure and properties of the elements.
Significance of Moseley's Experiment:
Moseley's work had profound implications for the understanding of the periodic table and the nature of the atom:
- Confirmation of Atomic Number: His experiment provided definitive experimental evidence that atomic number, not atomic mass, is the fundamental property that dictates the order of elements in the periodic table.
- Resolution of Anomalies: It explained the inconsistencies in the old periodic table based on atomic mass. For example, tellurium (atomic number 52) comes before iodine (atomic number 53) in Moseley's arrangement, which correctly aligns their properties in the periodic table.
- Foundation for the Modern Periodic Law: Moseley's findings directly led to the formulation of the Modern Periodic Law, which is based on arranging elements by increasing atomic number.
- Prediction of Missing Elements: By plotting the square root of the frequency against the atomic number, Moseley could identify gaps in the sequence, indicating the existence of undiscovered elements and their approximate atomic numbers.
- Understanding Atomic Structure: His work provided further insight into the structure of the atom, specifically the importance of the nucleus and the number of protons.
In conclusion, Moseley's experiment, coupled with his insightful mathematical analysis, revolutionized our understanding of the periodic table. He demonstrated convincingly that the atomic number is the fundamental property governing the chemical behavior of elements, leading to the formulation of the Modern Periodic Law and a more accurate and consistent representation of the relationships between the elements.
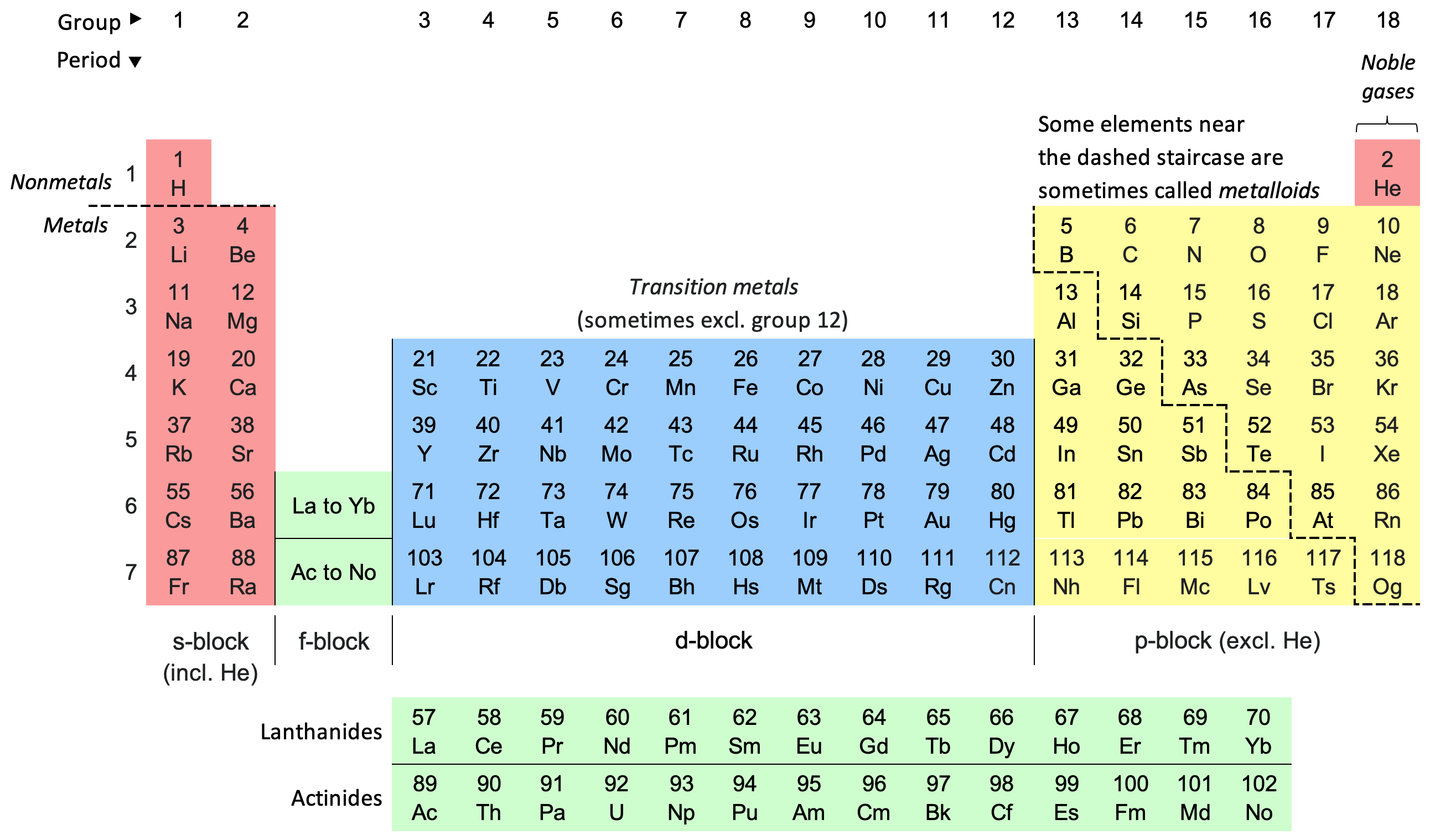
Let's break down the concepts of Periods and Groups in the periodic table:
Periods (Horizontal Rows) and Electron Shells
Periods are the seven horizontal rows in the periodic table. Elements within the same period share the same highest principal energy level (or electron shell) that their valence electrons occupy.
Think of it like building up electron shells around the nucleus. As you move across a period from left to right, electrons are being added to the same outermost electron shell.
-
Period Number and Electron Shell: The period number directly corresponds to the principal quantum number () of the outermost electron shell being filled.
For example:
- Elements in Period 1 have their valence electrons in the shell.
- Elements in Period 3 have their valence electrons in the shell.
- Generalizing this: , where is the principal quantum number of the outermost occupied electron shell.
-
Trends Across a Period: While elements in the same period have the same number of electron shells, the number of valence electrons increases as you move from left to right. This leads to significant changes in their chemical and physical properties. For example, metallic character generally decreases across a period, while non-metallic character increases.
Groups (Vertical Columns) and Valence Electrons
Groups (also known as families) are the 18 vertical columns in the periodic table. Elements within the same group share the same number of valence electrons (electrons in the outermost electron shell).
Valence electrons are the electrons primarily involved in chemical bonding and determine many of the chemical properties of an element. The similar number of valence electrons within a group leads to similarities in how these elements react and form compounds.
-
Group Number and Valence Electrons: For the main group elements (using the older A/B designation, which we'll discuss shortly), the group number often directly indicates the number of valence electrons. For the modern 1-18 numbering, the relationship is slightly different.
For example:
- Elements in Group 1 (alkali metals) have 1 valence electron.
- Elements in Group 17 (halogens) have 7 valence electrons.
- Generally: .
-
Trends Down a Group: While elements in the same group have the same number of valence electrons, the principal energy level of those valence electrons increases as you go down the group (meaning the electrons are in shells further from the nucleus). This affects properties like atomic size, ionization energy, and reactivity. For example, reactivity of alkali metals increases down the group.
Numbering Systems for Groups
There are two main systems used to number the groups in the periodic table:
1. The 1-18 System (IUPAC Designation):
-
This is the modern, internationally accepted system recommended by the International Union of Pure and Applied Chemistry (IUPAC).
-
It numbers the groups consecutively from 1 to 18, moving from left to right across the periodic table.
-
This system is straightforward and avoids the ambiguities of the older system.
Example:
- The alkali metals are Group 1.
- The halogens are Group 17.
- The noble gases are Group 18.
2. The A/B Designation (Older System):
-
This is an older system, but you may still encounter it.
-
It uses Roman numerals (I to VIII) followed by the letters "A" and "B".
-
"A" groups represent the main group elements (also called representative elements). These are the elements in groups 1, 2, and 13-18 (or IA, IIA, and IIIA-VIIIA). The Roman numeral often corresponds to the number of valence electrons for these groups.
-
"B" groups represent the transition metals. These are the elements in groups 3-12 (or IIIB-IIB). The numbering of the B groups is more complex and doesn't directly correlate to the number of valence electrons in the same simple way.
-
There are some inconsistencies in the older system, particularly with the numbering of the transition metals.
Example:
- Alkali metals (Group 1) are Group IA.
- Alkaline earth metals (Group 2) are Group IIA.
- Halogens (Group 17) are Group VIIA.
- Iron (Fe, in Group 8) is in Group VIIIB (along with Ru and Os).
- Zinc (Zn, in Group 12) is in Group IIB.
Correspondence between the two systems:
| IUPAC (1-18) | Older (A/B) |
|---|---|
| 1 | IA |
| 2 | IIA |
| 3 | IIIB |
| 4 | IVB |
| 5 | VB |
| 6 | VIB |
| 7 | VIIB |
| 8, 9, 10 | VIIIB |
| 11 | IB |
| 12 | IIB |
| 13 | IIIA |
| 14 | IVA |
| 15 | VA |
| 16 | VIA |
| 17 | VIIA |
| 18 | VIIIA |
In summary:
- Periods are horizontal rows, and elements in the same period have valence electrons in the same principal energy level.
- Groups are vertical columns, and elements in the same group have the same number of valence electrons, leading to similar chemical properties.
- The IUPAC 1-18 numbering system is the modern standard, while the A/B designation is an older system you may still encounter. Understanding both helps navigate different resources.
Blocks of Periodic Table
Let's explore the "blocks" of the periodic table, which categorize elements based on the sublevel of the outermost electron being filled. This provides a deeper understanding of the electron configurations and properties of elements.
Think of the electron shells having sublevels, denoted as s, p, d, and f. Each sublevel has a specific shape and capacity for electrons. The block an element belongs to tells us which of these sublevels is being filled with its valence electrons.
Here's a breakdown of each block:
1. s-block (Groups 1 & 2)
- Elements: This block comprises the elements in Group 1 (Alkali Metals) and Group 2 (Alkaline Earth Metals). Helium (He) in Group 18 is also technically an s-block element despite its placement.
- Electron Configuration: The outermost electrons of s-block elements occupy the s sublevel. They have a general valence electron configuration of ns1 (for Group 1) and ns2 (for Group 2 and Helium), where n is the principal quantum number (period number).
- Characteristics:
- Highly Reactive Metals (Groups 1 & 2): They readily lose their s-electrons to form positive ions with a +1 or +2 charge, respectively.
- Metallic Properties: Generally soft, silvery metals with good electrical and thermal conductivity.
- Low Ionization Energies: It takes relatively little energy to remove their outermost electrons.
- Helium (Unique): Although an s-block element, Helium is a noble gas with a completely filled 1s2 electron configuration, making it very unreactive.
2. p-block (Groups 13-18)
- Elements: This block includes the elements in Groups 13 (Boron Group) to 18 (Noble Gases).
- Electron Configuration: The outermost electrons of p-block elements are filling the p sublevel. They have a general valence electron configuration of ns2 np1-6.
- Characteristics:
- Diverse Properties: The p-block exhibits a wide range of properties, including metals, nonmetals, and metalloids (semimetals).
- Formation of Covalent and Ionic Compounds: They can gain, lose, or share electrons to form various types of chemical bonds.
- Increasing Non-metallic Character: Generally, non-metallic character increases as you move from left to right across the p-block.
- Noble Gases (Group 18): Have a completely filled p sublevel (ns2 np6, except Helium which is 1s2), making them very stable and unreactive.
3. d-block (Transition Metals)
- Elements: This block comprises the elements in Groups 3 to 12.
- Electron Configuration: The defining characteristic of d-block elements is that their outermost electrons are filling the (n-1)d sublevel. They also have electrons in the ns sublevel. Their general electron configuration is (n-1)d1-10 ns0-2.
- Characteristics:
- Metallic Properties: All d-block elements are metals, often hard, strong, and with high melting and boiling points.
- Variable Oxidation States: They can exhibit multiple positive oxidation states due to the involvement of both d and s electrons in bonding.
- Formation of Colored Compounds: Many of their compounds are colored due to the transitions of electrons within the d orbitals.
- Catalytic Activity: Many transition metals and their compounds act as good catalysts.
- Formation of Complex Ions: They readily form complex ions with ligands.
4. f-block (Lanthanides and Actinides)
- Elements: This block is located separately at the bottom of the periodic table and includes the Lanthanides (Period 6) and the Actinides (Period 7).
- Electron Configuration: The defining characteristic of f-block elements is that their outermost electrons are filling the (n-2)f sublevel. They also have electrons in the (n-1)d and ns sublevels. Their general electron configuration is (n-2)f1-14 (n-1)d0-1 ns2.
- Characteristics:
- Metallic Properties: All f-block elements are metals.
- Lanthanides (Rare Earth Metals): Shiny, silvery-white metals, relatively soft and reactive. They have very similar chemical properties due to their similar outer electron configurations.
- Actinides: All are radioactive. Some are naturally occurring, while others are synthetic. They exhibit a wider range of oxidation states compared to the lanthanides.
- Inner Transition Metals: Sometimes referred to as inner transition metals because the f sublevel is two energy levels below the outermost shell.
Visualizing the Blocks:
Imagine the periodic table as a neighborhood where the "streets" are the periods and the "avenues" are the groups. The blocks are like distinct sections of this neighborhood based on the type of electron "housing" being filled:
- s-block: The "entryway" on the left, accommodating the first two groups.
- p-block: The "right wing," housing the elements from Group 13 to 18.
- d-block: The "central section," containing the transition metals.
- f-block: Tucked away "internally," representing the lanthanides and actinides.
Relationship between Blocks and Orbitals:
The block an element belongs to directly correlates with the type of atomic orbital that the last electron added to its configuration occupies:
- s-block: Last electron enters an s orbital.
- p-block: Last electron enters a p orbital.
- d-block: Last electron enters a d orbital.
- f-block: Last electron enters an f orbital.
Understanding the blocks of the periodic table helps to predict and explain the chemical behavior and properties of elements based on their electron configurations and the orbitals being filled.
Key Groups and Their Properties
Alkali Metals (Group 1)
The alkali metals, residing in Group 1 of the periodic table (Lithium (Li), Sodium (Na), Potassium (K), Rubidium (Rb), Cesium (Cs), and Francium (Fr)), are a fascinating group of elements known for their vibrant reactivity and characteristic metallic properties. Their behavior is deeply rooted in their electronic configuration and exhibits striking periodic trends. Let's delve into the key aspects of these captivating elements.
Reactivity: Eager to React
The most defining characteristic of alkali metals is their exceptional reactivity. They are so reactive that they are never found in their free elemental form in nature, existing solely as compounds. This intense reactivity stems from their electronic structure: each alkali metal possesses a single valence electron in its outermost s orbital. This electron is loosely held by the nucleus due to the shielding effect of the inner electron shells. To achieve a stable noble gas configuration, alkali metals readily lose this single valence electron, forming a positively charged ion (cation) with a +1 charge.
The general reaction of an alkali metal (M) with water is a classic demonstration of their reactivity:
This reaction is exothermic, releasing heat and often enough energy to ignite the hydrogen gas produced. The vigor of this reaction increases as you descend the group. Lithium reacts relatively slowly, sodium reacts vigorously, potassium reacts with enough heat to ignite the hydrogen, and rubidium and cesium react explosively. Francium, being highly radioactive and rare, has not been studied as extensively, but its reactivity is predicted to be even greater.
Alkali metals also react readily with halogens (Group 17) to form metal halides, with oxygen to form various oxides (though the nature of the oxide varies down the group), and with hydrogen to form hydrides. These reactions are all characterized by the alkali metal losing its valence electron.
Metallic Properties: The Essence of Malleability and Conductivity
Alkali metals exhibit the typical properties of metals, although with some notable variations. They are silvery-white, lustrous solids when freshly cut, but they quickly tarnish in air due to their rapid reaction with oxygen and moisture. They are excellent conductors of heat and electricity, a hallmark of metallic bonding where valence electrons are delocalized and free to move throughout the metal lattice.
Unlike most metals, alkali metals are remarkably soft. They can be easily cut with a knife, with lithium being the hardest among them. This softness arises from the relatively weak metallic bonding due to the presence of only one valence electron per atom contributing to the "sea of electrons."
Other metallic properties include malleability (ability to be hammered into thin sheets) and ductility (ability to be drawn into wires), although their high reactivity makes it challenging to utilize these properties in practical applications. They also have relatively low melting and boiling points compared to other metals, again related to the weaker metallic bonding.
Common Compounds: Building Blocks of Chemistry
Alkali metals form a wide range of important compounds. Some notable examples include:
- Metal Halides: Formed by the direct reaction of alkali metals with halogens. Sodium chloride (NaCl), common table salt, is perhaps the most well-known. These are ionic compounds with high melting and boiling points, readily soluble in water.
- Metal Oxides: Alkali metals react with oxygen to form various oxides. Lithium primarily forms lithium oxide (). Sodium forms a mixture of sodium peroxide () and sodium oxide () when reacted with excess oxygen. Potassium, rubidium, and cesium tend to form superoxides () containing the superoxide ion ().
- Metal Hydroxides: Formed when alkali metals react with water (as shown in the reactivity equation). Sodium hydroxide (NaOH), also known as lye, and potassium hydroxide (KOH), or caustic potash, are strong bases widely used in industrial processes.
- Metal Carbonates and Bicarbonates: Sodium carbonate (), also known as washing soda, and sodium bicarbonate (), or baking soda, are common household chemicals with various applications.
- Metal Hydrides: Alkali metals react with hydrogen gas at high temperatures to form ionic hydrides, such as sodium hydride (NaH). These are strong reducing agents.
Periodic Trends: A Journey Down Group 1
The properties of alkali metals exhibit clear and predictable trends as you move down the group, reflecting the increasing atomic size and the changing influence of the nucleus on the valence electron.
-
Atomic Radii: Atomic radius increases down the group. This is because each subsequent element has an additional electron shell, increasing the distance of the outermost electron from the nucleus. For example, the atomic radius of lithium is significantly smaller than that of cesium.
-
Reactivity: Reactivity with water and other nonmetals increases down the group. While all alkali metals readily lose their valence electron, the ease with which this electron is lost increases down the group. This is attributed to two main factors:
- Decreasing Ionization Energy: The ionization energy, the energy required to remove an electron, decreases down the group. The larger atomic radius means the valence electron is further from the positively charged nucleus and experiences less attraction, making it easier to remove.
- Increasing Atomic Radius: The larger size also means that when reacting with another atom or molecule, the alkali metal atom has a greater surface area available for interaction.
-
Electronegativity: Electronegativity, the ability of an atom to attract electrons in a chemical bond, decreases down the group. As the atomic size increases, the valence electron is further from the nucleus and less tightly held, making it less effective at attracting electrons from other atoms. The electronegativity of lithium is higher than that of cesium. On the Pauling scale, lithium has an electronegativity of approximately 0.98, while cesium's is around 0.79.
-
Melting and Boiling Points: Melting and boiling points generally decrease down the group. This trend is related to the decreasing strength of metallic bonding. With only one valence electron contributing to the "sea of electrons," the attractive forces between the metal ions and the delocalized electrons weaken as the atomic size increases and the valence electrons become further from the nucleus.
-
Density: Density does not follow a perfectly consistent trend. While generally increasing down the group due to the increasing atomic mass, potassium is less dense than sodium. This is an exception attributed to the unique crystal structure of potassium.
In conclusion, the alkali metals are a group of remarkably reactive elements with characteristic metallic properties that are intricately linked to their electronic configuration. Their behavior beautifully illustrates the periodic trends that govern the properties of elements, making them a fundamental and fascinating subject in chemistry.
Alkali-Earth Metals (Groups 2)
Nestled next to the highly reactive alkali metals in the periodic table lies Group 2, the alkaline earth metals: Beryllium (Be), Magnesium (Mg), Calcium (Ca), Strontium (Sr), Barium (Ba), and Radium (Ra). These elements share similar chemical properties stemming from their electron configuration, exhibiting a compelling balance of reactivity and stability. Unlike their Group 1 neighbors, they possess two valence electrons in their outermost s orbital, a seemingly small difference that leads to significant variations in their behavior.
Reactivity: A Gradual Increase in Enthusiasm
Alkaline earth metals are reactive, though generally less so than alkali metals. Their reactivity is primarily driven by their tendency to lose their two valence electrons to achieve a stable noble gas configuration, forming positively charged ions (cations) with a +2 charge.
The general reaction of an alkaline earth metal (M) with water can be represented as:
However, the vigor of this reaction varies considerably down the group. Beryllium (Be) is an exception, showing little to no reaction with water, even at high temperatures. Magnesium (Mg) reacts very slowly with cold water but reacts readily with hot water or steam. The remaining elements, Calcium (Ca), Strontium (Sr), and Barium (Ba), react increasingly vigorously with cold water, similar to the reactivity trend seen in alkali metals. Radium (Ra), being radioactive, is less studied, but its reactivity is expected to be high.
The reaction with oxygen follows a similar trend. While all alkaline earth metals react with oxygen to form metal oxides (), the rate of reaction varies. Magnesium, for instance, burns with a bright white light in air, a reaction used in flares. They also react with halogens to form metal halides () and with acids to produce hydrogen gas and a metal salt.
It's crucial to note the difference in reactivity compared to alkali metals. The alkaline earth metals require more energy to remove their two valence electrons (higher ionization energy) compared to the single valence electron of alkali metals. This contributes to their generally lower reactivity. However, once the +2 ion is formed, the greater charge leads to stronger ionic bonds in their compounds.
Metallic Properties: Stronger and Sturdier
Like alkali metals, alkaline earth metals exhibit typical metallic properties, but with some significant distinctions. They are silvery-white, lustrous solids (though they tarnish upon exposure to air due to reaction with oxygen and moisture). They are good conductors of heat and electricity, characteristic of metallic bonding.
However, alkaline earth metals are harder, denser, and have higher melting and boiling points than their corresponding alkali metals in the same period. This difference arises from the presence of two valence electrons per atom, contributing to stronger metallic bonding. The "sea of electrons" is denser, leading to stronger attractive forces between the positively charged metal ions and the delocalized electrons. While still malleable and ductile, they are less so than alkali metals.
Common Compounds: Building Blocks of Nature and Industry
Alkaline earth metals form a diverse array of important compounds, many of which are crucial in both natural processes and industrial applications. Some key examples include:
- Metal Oxides: Formed by the direct reaction with oxygen. Magnesium oxide (MgO) is a refractory material used in furnace linings. Calcium oxide (CaO), also known as quicklime, is a crucial component of cement and is used in agriculture to adjust soil pH.
- Metal Hydroxides: Formed when the metals react with water (for the more reactive elements) or by reacting metal oxides with water. Calcium hydroxide (), or slaked lime, is used in mortar and plaster. Magnesium hydroxide () is a common ingredient in antacids (milk of magnesia).
- Metal Halides: Formed by reacting the metals with halogens. Calcium chloride () is used as a de-icer and drying agent. Magnesium chloride () is found in seawater.
- Carbonates and Sulfates: Calcium carbonate () is ubiquitous in nature, forming limestone, marble, and chalk. It's also a key ingredient in cement. Magnesium carbonate () is found in minerals like magnesite. Calcium sulfate () exists as gypsum and anhydrite and is used to make plaster of Paris.
- Organometallic Compounds: While less prevalent than for some other metals, alkaline earth metals do form organometallic compounds. Grignard reagents, containing magnesium, are important tools in organic synthesis.
Periodic Trends: Following the Downward Path
The properties of alkaline earth metals also exhibit clear periodic trends as you descend the group, mirroring, but with key differences, the trends observed in alkali metals.
-
Atomic Radii: Atomic radius increases down the group. This is because each subsequent element has an additional electron shell, increasing the distance of the outermost electrons from the nucleus.
-
Reactivity: Reactivity with water and other nonmetals generally increases down the group (with Beryllium as an exception). This is primarily due to:
- Decreasing Ionization Energy: The first ionization energy, the energy required to remove the first electron, and the second ionization energy, the energy required to remove the second electron, both decrease down the group. This makes it progressively easier to remove the two valence electrons.
- Increasing Atomic Radius: Similar to alkali metals, the larger size offers a greater surface area for interaction.
-
Electronegativity: Electronegativity decreases down the group. As the atomic size increases, the valence electrons are further from the nucleus and less tightly held, reducing their ability to attract electrons in a chemical bond. For example, Beryllium has a higher electronegativity (around 1.57 on the Pauling scale) than Barium (around 0.89).
-
Ionization Energy: Both the first and second ionization energies decrease down the group, as explained in the reactivity section. While the second ionization energy is always higher than the first (it's harder to remove a positive ion's electron), the trend remains downward.
-
Melting and Boiling Points: The trend for melting and boiling points is less consistent than in Group 1. While there is a general trend of decreasing melting and boiling points down the group from Magnesium onwards, Beryllium exhibits unexpectedly high values. This anomaly is attributed to its small size and strong covalent character in its metallic bonding.
-
Density: Density generally increases down the group due to the increasing atomic mass.
In summary, the alkaline earth metals occupy a fascinating middle ground between the extreme reactivity of alkali metals and the less reactive transition metals. Their two valence electrons dictate their tendency to form +2 cations and contribute to their characteristic metallic properties, which are generally stronger than those of alkali metals. Their diverse compounds play vital roles in both the natural world and human endeavors, and their periodic trends offer a valuable illustration of the principles governing the behavior of elements.
Transition Metals (d-block)
Occupying the central block of the periodic table, the transition metals, also known as the d-block elements, are a diverse group exhibiting a fascinating array of properties that make them essential components in various aspects of our lives. Their unique electronic configurations, characterized by partially filled d orbitals, are the key to their distinctive behaviors, including variable oxidation states, the formation of colored compounds, and remarkable catalytic activity. Let's delve into the intricacies of these versatile elements and their periodic trends.
Variable Oxidation States: A Tale of Multiple Electrons
A defining characteristic of transition metals is their ability to exhibit multiple oxidation states. Unlike the s-block elements, where the number of valence electrons dictates a fixed charge, transition metals can lose varying numbers of electrons from both their outermost s and inner (n-1)d orbitals. The energy difference between these orbitals is relatively small, allowing for the participation of d electrons in bonding.
For example, consider manganese (Mn), which can exhibit oxidation states ranging from -3 to +7. Common oxidation states include +2 (), +4 (), and +7 (). Similarly, iron (Fe) commonly exists as +2 () and +3 (), and can also achieve higher oxidation states like +6 in specific compounds.
The availability of multiple oxidation states is crucial for the diverse chemistry of transition metals. It enables them to form a wide variety of compounds with different properties and react under various conditions. Generally, lower oxidation states are more stable with electropositive elements, while higher oxidation states tend to be more stable when combined with highly electronegative elements like oxygen or fluorine. For instance, manganese(VII) exists as the permanganate ion (), a powerful oxidizing agent.
Colored Compounds: A Spectacle of Electronic Transitions
Many compounds of transition metals are vividly colored, a stark contrast to the typically colorless compounds of s-block elements. This phenomenon arises from the presence of partially filled d orbitals. When ligands (ions or molecules) surround a transition metal ion, the d orbitals are no longer degenerate (having the same energy). They split into sets of orbitals with slightly different energy levels.
When visible light passes through a transition metal compound, electrons in the lower energy d orbitals can absorb photons of specific wavelengths and get excited to higher energy d orbitals. This process is known as a d-d transition. The wavelengths of light absorbed correspond to specific colors, and the unabsorbed wavelengths are transmitted or reflected, giving the compound its characteristic color.
The color of a transition metal compound is influenced by several factors, including:
- The nature of the metal ion: Different metal ions have different d orbital splitting patterns, leading to different colors. For example, ions are typically blue, while ions are often violet or green.
- The oxidation state of the metal ion: Changing the oxidation state alters the number of d electrons and the ligand field strength, thus affecting the color. For instance, vanadium exhibits different colors in its different oxidation states.
- The nature of the ligands: Different ligands cause varying degrees of d orbital splitting. Strong field ligands cause a larger splitting, leading to the absorption of higher energy (shorter wavelength) light, while weak field ligands cause smaller splitting, absorbing lower energy (longer wavelength) light.
This ability to form colored compounds makes transition metals essential components in pigments, dyes, and gemstones.
Catalytic Activity: Speeding Up Reactions with Precision
Transition metals and their compounds are renowned for their exceptional catalytic activity, playing a vital role in numerous industrial processes and biological systems. Their ability to act as catalysts stems from several factors:
- Variable Oxidation States: The ability to readily change oxidation states allows transition metals to provide pathways with lower activation energies for reactions. They can readily accept and donate electrons, facilitating electron transfer processes crucial in many reactions.
- Ability to Form Complexes: Transition metals can form coordination complexes with reactant molecules, bringing them together in a favorable orientation for reaction. This interaction weakens existing bonds in the reactants and facilitates the formation of new bonds.
- Providing a Surface for Reactions (Heterogeneous Catalysis): Many transition metals act as heterogeneous catalysts, where the catalyst is in a different phase from the reactants. The surface of the metal provides active sites where reactants can adsorb, interact, and form products. This is crucial in processes like the Haber-Bosch process for ammonia synthesis (using iron as a catalyst) and catalytic converters in vehicles (using platinum, palladium, and rhodium).
Examples of transition metals and their catalytic roles include:
- Iron (Fe): Catalyst in the Haber-Bosch process for ammonia production.
- Nickel (Ni): Catalyst in the hydrogenation of unsaturated hydrocarbons.
- Platinum (Pt), Palladium (Pd), Rhodium (Rh): Catalysts in catalytic converters for reducing harmful emissions from vehicles.
- Vanadium(V) oxide (): Catalyst in the Contact process for sulfuric acid production.
- Manganese (Mn): Essential cofactor in many enzymes, acting as a biological catalyst.
Periodic Trends: Navigating the d-Block Landscape
The properties of transition metals exhibit interesting periodic trends, though they are not always as straightforward as those observed in the s and p blocks due to the involvement of inner d electrons.
-
Atomic Radii: Across a period, the atomic radii of transition metals generally decrease initially due to the increasing nuclear charge attracting the electrons more strongly. However, the decrease becomes less pronounced and may even slightly increase towards the end of the series. This is attributed to increased electron-electron repulsions in the d orbitals. Down a group, atomic radii increase due to the addition of electron shells.
-
Ionization Energy: The ionization energy generally increases across a period due to the increasing nuclear charge and decreasing atomic radius. However, there are irregularities due to the stability of certain d electron configurations (e.g., half-filled or fully filled d orbitals). Down a group, ionization energy generally decreases due to the increasing atomic radius and increased shielding of the outer electrons.
-
Electronegativity: Electronegativity generally increases across a period as the nuclear charge increases and atomic radius decreases, making it easier for the atom to attract electrons. Down a group, electronegativity generally decreases due to the increasing atomic radius and increased shielding.
-
Melting and Boiling Points: Transition metals generally have high melting and boiling points compared to s-block elements. This is due to the strong metallic bonding involving both s and d electrons. The number of unpaired d electrons influences the strength of metallic bonding, with elements in the middle of the series (like tungsten) often having the highest melting and boiling points due to the maximum number of unpaired d electrons available for bonding.
-
Density: Density generally increases across a period due to the increasing atomic mass and relatively small change in atomic volume. Down a group, density also generally increases.
In conclusion, transition metals are a fascinating and industrially vital group of elements whose unique properties stem from their partially filled d orbitals. Their variable oxidation states, ability to form colored compounds, and exceptional catalytic activity make them indispensable in a wide range of applications. Understanding their periodic trends provides a framework for predicting and explaining their diverse chemical behaviors.
Halogens (Group 17)
The halogens, residing in Group 17 of the periodic table – Fluorine (F), Chlorine (Cl), Bromine (Br), Iodine (I), and Astatine (At) – are a fascinating family of nonmetals renowned for their high reactivity and characteristic properties. Their name, derived from the Greek words meaning "salt-formers," aptly describes their tendency to react with metals to form salts. Their eagerness to gain an electron dictates much of their chemical behavior and gives rise to distinct periodic trends.
Reactivity: Eager Electron Grabbers
The hallmark of halogens is their exceptional reactivity, making them potent oxidizing agents. This stems from their electronic configuration: each halogen atom has seven valence electrons in its outermost p orbitals, needing only one more electron to achieve a stable noble gas configuration. This strong desire to gain an electron drives their reactions.
Halogens readily react with metals to form ionic compounds called metal halides. For example, sodium reacts vigorously with chlorine to form sodium chloride (table salt):
The reactivity of halogens decreases as you descend the group. Fluorine is the most reactive halogen, reacting explosively with almost all elements. Chlorine is also highly reactive, while bromine and iodine are less so. Astatine, being radioactive and rare, has not been studied extensively, but its reactivity is predicted to be the lowest among the group.
Halogens also react with hydrogen to form hydrogen halides (). The reaction with hydrogen is most vigorous for fluorine and less so for iodine:
(where X is a halogen)
These hydrogen halides are acidic in aqueous solutions. For instance, hydrogen chloride (HCl) forms hydrochloric acid, a strong acid. The acid strength generally increases down the group (HF being a notable exception due to strong hydrogen bonding).
Furthermore, halogens can react with each other to form interhalogen compounds, such as chlorine monofluoride () or bromine pentafluoride ().
Diatomic Molecules: Paired for Stability
Halogens exist in nature as diatomic molecules (), where two halogen atoms share a pair of electrons to form a single covalent bond. This pairing allows each atom to achieve a stable octet of electrons in its valence shell.
The physical state of the halogens at room temperature varies down the group:
- Fluorine (): A pale yellow-green gas.
- Chlorine (): A yellow-green gas.
- Bromine (): A reddish-brown liquid.
- Iodine (): A dark purple-black solid that sublimes to form a violet vapor.
- Astatine (): Predicted to be a solid, but due to its radioactivity and short half-life, it has not been observed in its elemental form.
The increasing size and number of electrons down the group lead to stronger London dispersion forces between the molecules, resulting in the transition from gaseous to liquid to solid states.
Common Compounds: Versatile Building Blocks
Halogens form a vast array of important compounds with diverse applications. Some prominent examples include:
- Hydrogen Halides (HX): As mentioned, these are acidic gases. Hydrochloric acid (HCl) is a crucial industrial chemical. Hydrofluoric acid (HF), despite being a weak acid, can etch glass.
- Metal Halides (MX): These are ionic compounds formed by the reaction of halogens with metals. Sodium chloride (NaCl), potassium iodide (KI), and silver bromide (AgBr) are well-known examples. Silver halides are light-sensitive and used in traditional photography.
- Interhalogen Compounds (): These are formed between two different halogens. Their properties vary depending on the halogens involved. Examples include , , and .
- Oxyacids and Oxoanions: Halogens form a series of oxyacids where the halogen is bonded to one or more oxygen atoms, and one oxygen atom is bonded to a hydrogen atom (e.g., hypochlorous acid, ; chloric acid, ). The corresponding anions are called oxoanions (e.g., hypochlorite ion, ; chlorate ion, ). These compounds have varying oxidizing strengths.
Periodic Trends: A Downward Shift in Properties
The properties of halogens exhibit clear and predictable trends as you move down the group, reflecting the increasing atomic size and the changing influence of the nucleus on the valence electrons.
-
Atomic Radii: Atomic radius increases down the group. This is because each subsequent element has an additional electron shell, increasing the distance of the outermost electrons from the nucleus.
-
Ionization Energy: Ionization energy, the energy required to remove an electron from an atom, decreases down the group. The valence electrons are further from the nucleus and experience greater shielding from the inner electron shells, making them easier to remove.
-
Electron Gain Enthalpy: Electron gain enthalpy refers to the change in energy when an electron is added to a neutral atom to form a negative ion. For halogens, this process is highly exothermic (negative value) because they readily accept an electron to achieve a stable octet. The electron gain enthalpy becomes less negative down the group from chlorine onwards. Interestingly, fluorine has a less negative electron gain enthalpy than chlorine. This is due to the small size of the fluorine atom; the incoming electron experiences significant electron-electron repulsion in the compact 2p subshell, making the process slightly less favorable than for chlorine, which has a larger 3p subshell. Therefore, chlorine has the most negative electron gain enthalpy.
-
Electronegativity: Electronegativity, the ability of an atom to attract electrons in a chemical bond, decreases down the group. As the atomic size increases, the valence electrons are further from the nucleus and less tightly held, reducing their ability to attract electrons from other atoms. Fluorine is the most electronegative element in the entire periodic table.
-
Reactivity: As mentioned earlier, reactivity as oxidizing agents decreases down the group. This trend is consistent with the decreasing electronegativity and electron gain enthalpy (after chlorine), making it less favorable for the heavier halogens to gain an electron. The increasing ionization energy also plays a role, as removing an electron from a halide ion becomes more difficult down the group, making them less effective reducing agents.
-
Melting and Boiling Points: Melting and boiling points increase down the group. This is due to the increasing strength of London dispersion forces between the diatomic molecules. Larger molecules with more electrons have stronger temporary dipoles, leading to stronger intermolecular attractions that require more energy to overcome during melting and boiling.
In summary, the halogens are a group of highly reactive nonmetals characterized by their eagerness to gain an electron. Their properties, from their diatomic nature to their ability to form a wide range of compounds, are dictated by their electron configuration and exhibit clear and predictable periodic trends. Their strong oxidizing power and ability to form salts make them crucial elements in various chemical processes and industrial applications.
Noble Gases (Group 18)
The noble gases, also known as the inert gases or rare gases, occupy the final column of the periodic table, Group 18: Helium (He), Neon (Ne), Argon (Ar), Krypton (Kr), Xenon (Xe), and Radon (Rn). Their defining characteristic is their remarkable chemical inertness, a property that stems directly from their unique electronic configuration. This stability has led to various important applications, leveraging their unreactive nature.
Inertness: The Hallmark of Stability
The most striking feature of the noble gases is their exceptional lack of chemical reactivity. For a long time, they were considered entirely inert, a notion that has been somewhat revised with the discovery of compounds involving the heavier noble gases. However, their general disinclination to form chemical bonds remains a cornerstone of their chemistry.
This inertness arises from their electronic structure: noble gases possess a full valence shell. With the exception of helium, which has a complete outer shell of two electrons (), the other noble gases have eight valence electrons in their outermost s and p orbitals (). This electron configuration, often referred to as a stable octet (or duet for helium), represents a state of minimal energy and maximum stability.
Due to their full valence shells, noble gases have:
-
High Ionization Energy: It requires a significant amount of energy to remove an electron from a noble gas atom because doing so disrupts the stable, filled outer shell. This indicates a strong hold on their electrons and a reluctance to form positive ions (cations).
-
Near-Zero Electron Affinity: Noble gas atoms have little or no tendency to accept an additional electron. Adding an electron would require placing it in a higher energy level, which is energetically unfavorable. This reflects their reluctance to form negative ions (anions).
-
Electronegativity Approaching Zero: Electronegativity is a measure of an atom's ability to attract electrons in a chemical bond. Since noble gases have little tendency to form bonds, their electronegativity values are extremely low, essentially zero.
-
Lack of Unpaired Electrons: All the electrons in the valence shell of noble gases are paired. This absence of unpaired electrons makes it difficult for them to form typical covalent bonds, which involve the sharing of unpaired electrons.
Full Valence Shell: The Root of Inertness
The concept of the full valence shell is central to understanding the inertness of noble gases. The stable electron configuration means that noble gas atoms are already in a state of low energy. They do not need to gain, lose, or share electrons to achieve stability, unlike most other elements.
The filled s and p subshells create a symmetrical distribution of electron density around the nucleus, resulting in a stable and non-polarizable electron cloud. This further contributes to their reluctance to interact with other atoms.
While the lighter noble gases (Helium, Neon, Argon) are truly exceptionally inert, under extreme conditions, the heavier noble gases (Krypton, Xenon, Radon) can be forced to form compounds, primarily with highly electronegative elements like fluorine and oxygen. This is because their outer electrons are further from the nucleus and experience greater shielding, making them slightly easier to involve in bonding. For example, xenon can form compounds like xenon tetrafluoride () and xenon trioxide (). Krypton difluoride () is another example of a noble gas compound. These compounds are often highly reactive and require specific conditions for their formation.
Applications: Leveraging Inertness
The very property that makes noble gases chemically unreactive also makes them invaluable for a wide range of applications where an inert atmosphere or medium is required. Some prominent applications include:
-
Lighting:
- Incandescent Bulbs: Argon is used to fill incandescent light bulbs to prevent the hot filament from oxidizing and burning out. Its inert nature extends the lifespan of the bulb.
- Neon Signs: Neon gas emits a bright reddish-orange light when an electric current is passed through it, hence its use in advertising signs. Different noble gases or mixtures produce various colors (e.g., argon for blue, krypton for greenish-white).
- Discharge Lamps: Krypton and xenon are used in high-intensity discharge lamps, such as those found in car headlights and photographic flashes, due to their ability to produce bright white light.
-
Welding: Argon and helium are used as shielding gases in welding. They create an inert atmosphere around the welding arc and molten metal, preventing oxidation and contamination by atmospheric gases like oxygen and nitrogen, which can weaken the weld.
-
Space Exploration: Liquid helium's extremely low boiling point makes it essential as a coolant for rocket fuels (liquid hydrogen and liquid oxygen) and for cooling instruments in satellites and spacecraft. Xenon is used as a propellant in ion thrusters for spacecraft due to its high atomic mass and inertness.
-
Cryogenics: Helium has the lowest boiling point of any element ( or ). This makes it indispensable as a cryogenic refrigerant for cooling superconductors in MRI machines, scientific research, and other low-temperature applications.
-
Leak Detection: Helium's small atomic size and inertness make it ideal for leak detection. It can penetrate very small leaks, and its presence can be easily detected by specialized instruments.
-
Medical Applications:
- MRI Cooling: As mentioned, liquid helium is vital for cooling the superconducting magnets in Magnetic Resonance Imaging (MRI) machines.
- Anesthesia: Xenon has anesthetic properties and is being researched as a safer alternative to some traditional anesthetics.
-
Research and Industry: Noble gases are used to create inert atmospheres in laboratories and industrial processes where reactions with oxygen or nitrogen need to be avoided. Argon is frequently used as a blanket gas in chemical reactions.
Periodic Trends:
While noble gases are characterized by their inertness, their physical properties exhibit predictable periodic trends:
-
Atomic Radii: Atomic radius increases down the group. This is due to the addition of electron shells, increasing the distance of the outermost electrons from the nucleus.
-
Ionization Energy: Ionization energy decreases down the group. The valence electrons are further from the nucleus and experience greater shielding, making them easier to remove. This explains why the heavier noble gases are slightly more reactive.
-
Boiling Point: Boiling point increases down the group. This is due to the increasing strength of London dispersion forces between the atoms. Larger atoms with more electrons have stronger temporary dipoles, leading to stronger intermolecular attractions.
-
Density: Density increases down the group, primarily due to the increasing atomic mass.
In conclusion, the noble gases stand out for their exceptional chemical inertness, a direct consequence of their full valence electron shells. This stability has led to a plethora of applications, leveraging their unreactive nature in diverse fields. While traditionally considered completely inert, the heavier noble gases' ability to form compounds under specific conditions highlights the nuanced nature of chemical bonding and the power of extreme conditions. Their predictable periodic trends, despite their inertness, further solidify their place within the systematic organization of the periodic table.
F. Other Notable Groups/Elements
Beyond the main groups, the periodic table houses other fascinating categories of elements with unique characteristics and significant importance. Let's explore the Chalcogens, Metalloids/Semiconductors, and Rare Earth Elements.
1. Chalcogens (Group 16): The Ore-Formers
The Chalcogens, residing in Group 16 (also known as the oxygen family), consist of Oxygen (O), Sulfur (S), Selenium (Se), Tellurium (Te), and Polonium (Po). The name "chalcogen" comes from the Greek words meaning "ore-forming," reflecting their tendency to be found in ores of various metals.
-
Electronic Configuration & Reactivity: Chalcogens have six valence electrons in their outermost s and p orbitals (). They need two more electrons to achieve a stable octet, making them reactive nonmetals, although less reactive than the halogens. They tend to gain two electrons to form anions with a -2 charge, but can also exhibit other oxidation states.
-
Diatomic and Polyatomic Forms: Oxygen exists primarily as a diatomic molecule (), essential for respiration, and also as ozone (). Sulfur can form various allotropes, including the common cyclic ring. Selenium and tellurium also form polymeric structures.
-
Common Compounds:
- Oxides: Chalcogens readily react with most elements to form oxides. Water () is arguably the most crucial oxide. Sulfur dioxide () and sulfur trioxide () are important in industrial processes and environmental issues like acid rain.
- Sulfides, Selenides, Tellurides: These are compounds formed with less electronegative elements. Metal sulfides like iron sulfide () and zinc sulfide () are common ores.
- Acids: Sulfur forms important oxyacids like sulfuric acid (), a vital industrial chemical.
-
Periodic Trends:
- Atomic Radii: Atomic radius increases down the group due to the addition of electron shells.
- Ionization Energy: Ionization energy decreases down the group, making it easier to remove an electron.
- Electron Gain Enthalpy: Oxygen has a less negative electron gain enthalpy than sulfur due to its small size and electron repulsion. Electron gain enthalpy becomes less negative down the group from sulfur onwards.
- Electronegativity: Electronegativity decreases down the group, making oxygen the second most electronegative element after fluorine.
- Metallic Character: Metallic character increases down the group. Oxygen and sulfur are nonmetals, selenium is a metalloid, and tellurium and polonium exhibit more metallic properties.
-
Applications: Oxygen is vital for life and combustion. Sulfur is used in sulfuric acid production, vulcanization of rubber, and various other industrial processes. Selenium is used in photocopiers, solar cells, and as a dietary supplement. Tellurium is used in solar cells and alloys. Polonium is radioactive and has limited applications.
2. Metalloids/Semiconductors (Diagonal Region): The Balancing Act
Located along the "stairstep" diagonal line separating metals and nonmetals on the periodic table, the metalloids (also known as semimetals) exhibit properties intermediate between those of metals and nonmetals. The most commonly recognized metalloids are Boron (B), Silicon (Si), Germanium (Ge), Arsenic (As), Antimony (Sb), and Tellurium (Te) (which is also considered a chalcogen).
-
Intermediate Properties: Metalloids exhibit some metallic characteristics (like luster and electrical conductivity) and some nonmetallic characteristics (like brittleness and variable ionization energies). Their defining property is their semiconductivity.
-
Semiconductivity: Unlike conductors (metals) which conduct electricity readily, and insulators (nonmetals) which do not, semiconductors have an electrical conductivity between the two. Their conductivity can be increased by adding impurities, a process called doping. This unique property is crucial for modern electronics.
-
Common Examples and Applications:
- Silicon (Si): The most well-known semiconductor, the foundation of modern electronics. Used in transistors, integrated circuits (computer chips), solar cells, and many other electronic devices. Silicon dioxide () is the main component of sand and quartz.
- Germanium (Ge): Another important semiconductor, historically used in early transistors. Now used in some specialized applications like infrared optics and certain alloys.
- Boron (B): While not a semiconductor in its pure form, boron compounds are used in various applications, including borosilicate glass (Pyrex) and detergents. Boron can be doped into silicon to alter its conductivity.
- Arsenic (As): A toxic metalloid, used in some alloys and as a dopant in semiconductors. Gallium arsenide (GaAs) is a semiconductor with applications in high-speed electronics and LEDs.
- Antimony (Sb): Used in alloys to increase hardness and in flame retardants.
- Tellurium (Te): As mentioned, also a chalcogen. Used in solar cells and thermoelectric devices.
-
Periodic Trends (General): The trends across the metalloid region are transitional. Moving from left to right, metallic character decreases, ionization energy and electronegativity increase. Moving down a group, metallic character generally increases.
-
Importance: Metalloids are indispensable in modern technology, particularly in electronics and materials science. Their semiconducting properties have revolutionized computing, communication, and countless other aspects of modern life.
3. Rare Earth Elements (Lanthanides and Actinides): The Inner Transition Metals
Located in the f-block of the periodic table, the Rare Earth Elements (REEs) consist of two series: the Lanthanides and the Actinides. They are called "rare earth" not because they are exceptionally scarce, but because they are often found together in minerals and their separation is complex.
-
Lanthanides (Atomic Numbers 57-71): These elements follow Lanthanum (La) and involve the filling of the 4f subshell. They share very similar chemical properties due to their outer electron configurations being almost identical. They are silvery-white, reactive metals that readily tarnish in air.
- Key Characteristics: High melting and boiling points, form +3 ions predominantly, strong paramagnetism for some.
- Applications: Used in high-strength magnets (neodymium and samarium magnets), lasers (neodymium, erbium), phosphors for screens and lighting (europium, terbium), catalysts, and as components in various alloys.
-
Actinides (Atomic Numbers 89-103): These elements follow Actinium (Ac) and involve the filling of the 5f subshell. All actinides are radioactive, and many are synthetic (transuranium elements).
- Key Characteristics: Radioactivity is the dominant feature. Exhibit multiple oxidation states.
- Applications: Uranium (U) and Plutonium (Pu) are crucial in nuclear power generation and nuclear weapons. Thorium (Th) is a potential nuclear fuel. Americium (Am) is used in smoke detectors. Other actinides are primarily used in research.
-
Electronic Configuration: Lanthanides have the general configuration , and Actinides have . The filling of the inner f-orbitals is responsible for their characteristic properties.
-
Periodic Trends (Within Series): Within the lanthanides, there is a phenomenon called the "lanthanide contraction," where the atomic and ionic radii decrease slightly but steadily across the series due to the poor shielding of the 4f electrons. Similar contraction exists for actinides.
-
Importance: Rare earth elements, despite their name, are critical components in many modern technologies, including electronics, renewable energy, and defense applications. Actinides play a significant role in nuclear energy and related fields. However, the extraction and processing of rare earth elements can have environmental challenges.
These diverse groups of elements, beyond the main blocks, contribute significantly to the richness and complexity of chemistry and the world around us. Understanding their unique properties and behaviors is essential for advancing scientific knowledge and technological innovation.
Periodic Trends
Atomic radius refers to the typical distance from the center of the nucleus to the boundary of the surrounding cloud of electrons. However, the electron cloud does not have a sharp boundary, so different methods are used to define and measure atomic radius. There are four main types of atomic radii:
A. Types of Atomic Radii
1. Covalent Radius
The covalent radius is defined as one-half the distance between the nuclei of two identical atoms joined by a single covalent bond. This is the most commonly used type of atomic radius for non-metals.
Example: In a diatomic chlorine molecule (), the distance between the nuclei of the two chlorine atoms is experimentally determined to be approximately . Therefore, the covalent radius of a chlorine atom is:
For a diheteratomic molecule like , if we assume that the covalent radius is simply additive, the bond distance would be the sum of the covalent radii of the individual atoms:
However, due to differences in electronegativity, the actual bond distance can deviate from this simple sum. The equation provided in the prompt attempts to account for this deviation:
Here, is the bond distance between atoms A and B in a heteronuclear diatomic molecule, and are the covalent bond lengths in the respective homonuclear diatomic molecules ( and ), and is a term related to the electronegativity difference between A and B. This equation is not directly used to calculate the atomic radius but rather to estimate the bond length in a heteronuclear molecule based on the covalent bond lengths of the homonuclear molecules and their electronegativity difference.
To find the covalent radius of an atom in a heteronuclear molecule, we often rely on experimentally determined bond lengths and known covalent radii of other atoms. For example, if the bond length of is measured to be , and the covalent radius of is known to be , we can estimate the covalent radius of :
Covalent Radius Calculator
2. Metallic Radius
The metallic radius is defined as one-half the distance between the nuclei of two adjacent metal atoms in a metallic crystal lattice.
Example: In solid copper (), the distance between the nuclei of two adjacent copper atoms is found to be . Therefore, the metallic radius of a copper atom is:
3. Van der Waals Radius
The van der Waals radius is defined as one-half the distance of closest approach between two non-bonded atoms in separate molecules or noble gas atoms in a solid. This radius reflects the extent of the electron cloud around an atom and the repulsive forces that prevent atoms from getting too close.
Example: Consider two argon atoms () in separate molecules. The closest they can approach each other is determined by their van der Waals interactions. If the distance of closest approach is found to be , the van der Waals radius of an argon atom is:
It's important to note that the van der Waals radius is always larger than the covalent radius for the same atom because it represents a non-bonded interaction distance.
4. Ionic Radius
The ionic radius is the radius of an ion in an ionic crystal structure. The size of an ion is affected by the loss or gain of electrons.
-
Cations (positive ions): When an atom loses electrons to form a cation, it loses its outermost electron shell, and the remaining electrons are pulled closer to the nucleus due to the increased effective nuclear charge. Therefore, cations are smaller than their parent atoms.
Example: The atomic radius of sodium () is , while the ionic radius of sodium ion () is .
-
Anions (negative ions): When an atom gains electrons to form an anion, the increased electron-electron repulsion causes the electron cloud to expand, and the effective nuclear charge per electron decreases. Therefore, anions are larger than their parent atoms.
Example: The atomic radius of chlorine () is , while the ionic radius of chloride ion () is .
For a diheteratomic ionic compound like , the distance between the nuclei of and ions is the sum of their ionic radii:
B. Trends in Atomic Radius
1. Trend Down a Group
Trend: Atomic radius generally increases down a group (column) in the periodic table.
Explanation based on electron shielding and nuclear charge:
-
Increasing Principal Quantum Number: As you move down a group, electrons are added to higher principal energy levels (n). These higher energy levels correspond to electron shells that are further from the nucleus. This means the outermost electrons are located at a greater average distance from the nucleus, leading to a larger atomic radius.
-
Increased Electron Shielding: The inner electrons effectively shield the outer electrons from the full attractive force of the positively charged nucleus. As you go down a group, the number of inner electron shells increases. These inner electrons repel the outer electrons, reducing the effective nuclear charge experienced by the outermost electrons. Although the nuclear charge itself increases down the group (more protons), the effect of increased shielding is more significant in determining the atomic radius. The outer electrons are less tightly held, resulting in a larger atomic size.
2. Trend Across a Period
Trend: Atomic radius generally decreases across a period (row) in the periodic table from left to right.
Explanation based on electron shielding and nuclear charge:
-
Increasing Nuclear Charge: As you move across a period, the number of protons in the nucleus increases, leading to a greater positive charge. This increased nuclear charge exerts a stronger pull on the electrons.
-
Relatively Constant Shielding: Electrons added across a period are added to the same principal energy level (the same electron shell). The number of core electrons (inner shells) remains the same. Therefore, the shielding effect provided by the inner electrons remains relatively constant.
Since the nuclear charge increases while the shielding remains relatively constant, the effective nuclear charge experienced by the outermost electrons increases significantly. This stronger attraction pulls the electrons closer to the nucleus, resulting in a smaller atomic radius.
Ionic Radius
Ionic radius refers to the radius of a cation or an anion. The size of an ion is significantly different from the size of its parent atom due to the gain or loss of electrons.
Relationship between Atomic Radius and Ion Size
The formation of ions dramatically alters the size of the atom.
-
Cations (Positive Ions): When an atom loses one or more electrons to form a cation, the following occurs:
- Loss of the outermost electron shell: Often, the electrons lost are from the highest principal quantum number (). This results in the removal of the outermost electron shell, leading to a significant decrease in size.
- Increased effective nuclear charge: With fewer electrons, the remaining electrons experience a greater effective nuclear charge (the net positive charge experienced by an electron). This stronger attraction pulls the remaining electrons closer to the nucleus.
- Decreased electron-electron repulsion: Fewer electrons lead to less electron-electron repulsion, allowing the remaining electrons to be drawn closer to the nucleus.
Therefore, cations are significantly smaller than their parent atoms.
Example: The atomic radius of sodium () is . When sodium loses one electron to form a sodium ion (), it loses its outermost electron shell (). The ionic radius of is .
-
Anions (Negative Ions): When an atom gains one or more electrons to form an anion, the following occurs:
- Increased electron-electron repulsion: Adding electrons increases the repulsion between electrons in the valence shell. This repulsion forces the electron cloud to expand.
- Decreased effective nuclear charge per electron: Although the nuclear charge remains the same, the increased number of electrons means that each electron experiences a slightly smaller effective nuclear charge. The nucleus's pull is now distributed over more electrons.
Therefore, anions are significantly larger than their parent atoms.
Example: The atomic radius of chlorine () is . When chlorine gains one electron to form a chloride ion (), it now has a filled valence shell. The ionic radius of is .
Trends in Ionic Radius Down a Group
Trend: Ionic radius generally increases down a group for ions with the same charge.
Explanation:
- Increasing Principal Quantum Number: As you move down a group, the ions are formed from atoms with electrons in higher principal energy levels (). This means the outermost electrons (or the remaining outermost electrons in cations) are located in shells further from the nucleus.
- Increased Number of Electron Shells: With each successive element down the group, another electron shell is added to the ion (or the parent atom before ionization). This leads to a larger overall size of the electron cloud, even if the ion has lost electrons compared to its parent atom.
- Increased Electron Shielding: The increased number of inner electrons provides more effective shielding of the outer electrons from the nuclear charge. Although the nuclear charge also increases down the group, the increase in shielding is more significant in determining the size.
Examples:
-
Alkali Metal Cations (Group 1): () < () < () < () < ()
-
Halide Anions (Group 17): () < () < () < ()
Trends in Ionic Radius Across a Period
The trend in ionic radius across a period is more complex than the trend in atomic radius because we are comparing both cations and anions, and the change in charge also significantly affects size. However, we can observe trends within series of isoelectronic ions (ions with the same number of electrons).
Trend for Isoelectronic Ions: For a series of isoelectronic ions, ionic radius decreases with increasing nuclear charge (atomic number).
Explanation:
- Same Number of Electrons: Isoelectronic ions have the same electron configuration and therefore the same number of electrons.
- Increasing Nuclear Charge: As you move across a period, the number of protons in the nucleus increases, leading to a greater positive charge.
- Stronger Attraction: The increasing nuclear charge exerts a stronger pull on the fixed number of electrons. This stronger attraction draws the electron cloud closer to the nucleus, resulting in a smaller ionic radius.
Examples of Isoelectronic Series:
Consider the isoelectronic series with 10 electrons: , , , , , .
-
Nuclear Charges: N (7+), O (8+), F (9+), Na (11+), Mg (12+), Al (13+)
-
Ionic Radii (approximate): () > () > () > () > () > ()
As you move from to , the number of electrons remains the same, but the nuclear charge increases. This increasing positive charge pulls the electrons in more tightly, leading to a decrease in ionic radius.
Overall Trend Across a Period (Considering both Cations and Anions):
Across a period, you typically move from large metal atoms that lose electrons to form smaller cations, followed by non-metal atoms that gain electrons to form larger anions. The trend isn't strictly increasing or decreasing throughout the entire period, but rather exhibits a sharp decrease when moving from cations to anions and then a decrease among the cations and an increase among the anions.
For example, in Period 3:
> > (decreasing size among cations) > (decreasing size among anions - isoelectronic trend within the anions)
It's important to compare ions with the same charge or within isoelectronic series to observe a consistent trend across a period.
Ionization Energy
Definition of Ionization Energy
Ionization energy (IE), also known as ionization potential, is the minimum energy required to remove the most loosely bound electron from a neutral atom in its gaseous state. This process results in the formation of a positively charged ion (cation).
The process can be represented by the following equation:
Where:
- represents a neutral atom of element X in the gaseous state.
- is the first ionization energy, the energy required to remove the first electron.
- is the singly charged positive ion of element X in the gaseous state.
- is the removed electron.
Subsequent electrons can also be removed, requiring successively higher amounts of energy. These are called the second ionization energy (), third ionization energy (), and so on.
In general, the ionization energy () is the energy required to remove the electron from an atom or ion with a charge of .
Key Points about Ionization Energy:
- Ionization energy is always a positive value because energy is required to overcome the attraction between the positively charged nucleus and the negatively charged electron. It is an endothermic process.
- The magnitude of ionization energy is a measure of how strongly an atom holds onto its outermost electrons.
- Higher ionization energy indicates that it is more difficult to remove an electron.
- Ionization energy is typically measured in kilojoules per mole () or electron volts ().
Trends in Ionization Energy
1. Trend Down a Group
Trend: Ionization energy generally decreases down a group (column) in the periodic table.
Explanation:
The decrease in ionization energy down a group can be explained by considering the following factors:
- Increasing Atomic Radius: As you move down a group, the atomic radius increases. This means the outermost electrons are located further away from the nucleus.
- Increased Electron Shielding: The number of inner electron shells increases down a group. These inner electrons effectively shield the valence electrons from the full positive charge of the nucleus. The valence electrons experience a smaller effective nuclear charge.
- Decreased Nuclear Attraction: Due to the increased distance and shielding, the attractive force between the nucleus and the outermost electrons weakens.
Because the outermost electrons are further from the nucleus and experience less attraction, less energy is required to remove them.
Examples:
-
Group 1 (Alkali Metals): () > () > () > () > ()
-
Group 17 (Halogens): () > () > () > ()
2. Trend Across a Period
Trend: Ionization energy generally increases across a period (row) in the periodic table from left to right.
Explanation:
The increase in ionization energy across a period can be explained by:
- Decreasing Atomic Radius: As you move across a period, the atomic radius generally decreases. This means the outermost electrons are held closer to the nucleus.
- Increasing Effective Nuclear Charge: Across a period, the number of protons in the nucleus increases, while the number of inner electron shells remains the same. This leads to an increase in the effective nuclear charge experienced by the valence electrons.
- Stronger Nuclear Attraction: With a greater effective nuclear charge and smaller atomic radius, the attractive force between the nucleus and the outermost electrons becomes stronger.
Because the outermost electrons are closer to the nucleus and experience a stronger attraction, more energy is required to remove them.
Examples:
- Period 3: () < () < () < () < () < () < () < ()
Exceptions to the General Trend Across a Period:
There are some exceptions to the general increasing trend of ionization energy across a period, primarily due to the electron configurations of the elements.
-
Between Group 2 (Alkaline Earth Metals) and Group 13 (Boron Group): The ionization energy of Group 13 elements is slightly lower than that of Group 2 elements in the same period. This is because the electron being removed from a Group 13 element is in a subshell, which is higher in energy and slightly further from the nucleus than the electron being removed from a Group 2 element. The electron also experiences some shielding from the filled subshell.
- Example: () > ()
-
Between Group 15 (Nitrogen Group) and Group 16 (Oxygen Group): The ionization energy of Group 16 elements is slightly lower than that of Group 15 elements in the same period. This is due to the electron configuration of the Group 15 elements having a half-filled subshell (), which is a relatively stable arrangement due to the exchange energy. Removing an electron from this stable half-filled subshell requires more energy. In contrast, the Group 16 elements have a configuration, with one of the orbitals containing a paired electron. The repulsion between these paired electrons makes it slightly easier to remove one of them.
- Example: () > ()
These exceptions highlight the influence of electron configuration and orbital stability on ionization energy.
Electronegativity
Definition of Electronegativity
Electronegativity (EN) is a measure of the tendency of an atom to attract a shared pair of electrons towards itself in a chemical bond. It is a dimensionless property, although various scales have been developed to quantify it, with the Pauling scale being the most common. On the Pauling scale, fluorine (the most electronegative element) is assigned a value of 4.0.
Key Points about Electronegativity:
- Electronegativity describes the relative ability of an atom to attract electrons within a covalent bond.
- It is a concept that applies to atoms when they are bonded to other atoms.
- Higher electronegativity indicates a greater tendency of an atom to attract bonding electrons.
- The difference in electronegativity between two bonded atoms can provide insights into the polarity of the bond. A large difference in electronegativity leads to a polar covalent bond or an ionic bond.
Trends in Electronegativity
1. Trend Down a Group
Trend: Electronegativity generally decreases down a group (column) in the periodic table.
Explanation:
The decrease in electronegativity down a group can be attributed to the following factors:
- Increasing Atomic Radius: As you move down a group, the atomic radius increases. The valence electrons are located further away from the nucleus.
- Increased Electron Shielding: The number of inner electron shells increases, leading to greater shielding of the valence electrons from the positive charge of the nucleus. The effective nuclear charge experienced by the valence electrons decreases.
- Weaker Nuclear Attraction: Due to the increased distance and shielding, the nucleus has a weaker ability to attract the shared electrons in a bond.
With a weaker pull from the nucleus and the bonding electrons being further away, the atom has a lower tendency to attract those shared electrons towards itself.
Examples:
-
Group 17 (Halogens): (3.98) > (3.16) > (2.96) > (2.66) > (2.2) (Pauling scale values)
-
Group 1 (Alkali Metals): (0.98) > (0.93) > (0.82) > (0.82) > (0.79) (Pauling scale values)
2. Trend Across a Period
Trend: Electronegativity generally increases across a period (row) in the periodic table from left to right.
Explanation:
The increase in electronegativity across a period is due to:
- Decreasing Atomic Radius: As you move across a period, the atomic radius generally decreases. The valence electrons are held closer to the nucleus.
- Increasing Effective Nuclear Charge: Across a period, the number of protons in the nucleus increases, while the number of inner electron shells remains the same. This leads to an increase in the effective nuclear charge experienced by the valence electrons.
- Stronger Nuclear Attraction: With a greater effective nuclear charge and smaller atomic radius, the nucleus exerts a stronger attractive force on the bonding electrons.
The stronger pull from the nucleus makes the atom more capable of attracting the shared electrons in a bond towards itself.
Examples:
- Period 3: (0.93) < (1.31) < (1.61) < (1.90) < (2.19) < (2.58) < (3.16) < (No value typically assigned, noble gases generally do not form stable bonds) (Pauling scale values)
Important Considerations:
- Noble Gases: Noble gases (Group 18) generally have high ionization energies and very low or no tendency to form chemical bonds under normal conditions. Therefore, electronegativity values are not typically assigned to them.
- Metals vs. Non-metals: Metals generally have low electronegativity values, indicating their tendency to lose electrons. Non-metals generally have high electronegativity values, indicating their tendency to gain or share electrons and attract them strongly in a bond. Metalloids have intermediate electronegativity values.
- Relationship to Bond Polarity: The difference in
electronegativity between two bonded atoms determines the polarity of
the bond.
- Small difference (typically < 0.4): Nonpolar covalent bond
- Intermediate difference (typically 0.4 - 1.7): Polar covalent bond
- Large difference (typically > 1.7): Ionic bond
Understanding electronegativity trends helps predict the nature of chemical bonds and the distribution of electron density in molecules.
Metallic Character
Metallic character refers to the set of chemical properties associated with metals. These properties arise from the ability of metal atoms to easily lose electrons and form positive ions (cations). Key characteristics of metals include:
- Good conductors of heat and electricity: Due to the presence of delocalized electrons.
- Malleable and ductile: Can be hammered into thin sheets and drawn into wires, respectively, due to the ability of metal atoms to slide past each other without breaking bonds.
- Lustrous (shiny): Reflect light due to the interaction of light with the delocalized electrons.
- Tendency to lose electrons and form positive ions.
- Basic oxides: Their oxides react with acids to form salts and water.
The degree to which an element exhibits these properties is a measure of its metallic character.
Trends in Metallic Character
The trends in metallic character are inversely related to the trends in electronegativity and ionization energy. Elements with low ionization energies and low electronegativities readily lose electrons and exhibit strong metallic character.
1. Trend Down a Group
Trend: Metallic character generally increases down a group (column) in the periodic table.
Explanation:
The increase in metallic character down a group can be explained by considering the following factors:
- Decreasing Ionization Energy: As you move down a group, the ionization energy decreases. This means it becomes easier for atoms to lose their outermost electrons.
- Increasing Atomic Radius: The atomic radius increases down a group. The valence electrons are further from the nucleus and experience less attraction.
- Increased Electron Shielding: The number of inner electron shells increases, leading to greater shielding of the valence electrons from the positive charge of the nucleus. The effective nuclear charge decreases.
Because it becomes easier to lose electrons, the fundamental characteristic of metals, the metallic character increases down a group. The valence electrons are held more loosely and are more readily available to participate in metallic bonding or to be lost in chemical reactions.
Examples:
- Group 1 (Alkali Metals): Lithium (Li) is less metallic than Sodium (Na), which is less metallic than Potassium (K), and so on. Cesium (Cs) is the most metallic of the stable alkali metals.
- Group 13: Boron (B) is a metalloid, but aluminum (Al), gallium (Ga), indium (In), and thallium (Tl) are metals, with metallic character generally increasing down the group.
2. Trend Across a Period
Trend: Metallic character generally decreases across a period (row) in the periodic table from left to right.
Explanation:
The decrease in metallic character across a period is due to:
- Increasing Ionization Energy: As you move across a period, the ionization energy generally increases. This means it becomes more difficult for atoms to lose their outermost electrons.
- Decreasing Atomic Radius: The atomic radius decreases across a period. The valence electrons are held more tightly by the nucleus.
- Increasing Effective Nuclear Charge: The effective nuclear charge experienced by the valence electrons increases across a period.
As it becomes more difficult for atoms to lose electrons, their tendency to behave as metals decreases. Instead, they tend to gain electrons (non-metals) or share electrons (metalloids).
Examples:
- Period 3: Sodium (Na) is a very reactive metal, magnesium (Mg) is a reactive metal, aluminum (Al) is a metal, silicon (Si) is a metalloid, phosphorus (P), sulfur (S), and chlorine (Cl) are non-metals, and argon (Ar) is a noble gas. The metallic character clearly decreases across the period.
Relationship to Non-metallic Character:
The trend in metallic character is inversely related to the trend in non-metallic character. As metallic character decreases across a period, non-metallic character increases. Down a group, as metallic character increases, non-metallic character decreases.
Summary Table of Trends:
| Property | Trend Down a Group | Trend Across a Period | Explanation |
|---|---|---|---|
| Atomic Radius | Increases | Decreases | Increased electron shells & shielding vs. increased nuclear charge |
| Ionization Energy | Decreases | Increases | Easier to lose electrons due to size & shielding vs. harder to lose electrons due to increased nuclear charge |
| Electronegativity | Decreases | Increases | Weaker nuclear attraction vs. stronger nuclear attraction |
| Metallic Character | Increases | Decreases | Easier to lose electrons vs. harder to lose electrons |
| Non-metallic Char. | Decreases | Increases | Harder to gain electrons vs. easier to gain electrons |
Understanding the periodic trends in metallic character is crucial for predicting the chemical behavior of elements and for classifying them as metals, non-metals, or metalloids.
Reactivity Trends: Relating to Other Periodic Trends
Chemical reactivity describes the tendency of an atom or molecule to undergo a chemical reaction, either by itself or with other substances. Reactivity is fundamentally linked to the ability of atoms to achieve a stable electron configuration, typically a filled valence shell (octet rule for main group elements, or stable d-orbital configurations for transition metals). Therefore, reactivity trends are closely related to the periodic trends we've discussed so far.
We can analyze reactivity trends separately for metals and non-metals because their mechanisms for achieving stability differ: metals tend to lose electrons, while non-metals tend to gain electrons.
A. Reactivity of Metals
Metals react by losing electrons to form positive ions (cations). The ease with which a metal loses electrons determines its reactivity. Therefore, metallic reactivity is directly related to:
- Ionization Energy: A lower ionization energy means it takes less energy to remove an electron, making the metal more reactive.
- Electronegativity: A lower electronegativity indicates a weaker attraction for electrons, making it easier for the metal to lose electrons and form positive ions.
- Atomic Radius: Larger atomic radii generally correspond to lower ionization energies (outer electrons are further from the nucleus and less tightly held), contributing to higher reactivity.
Trends in Metallic Reactivity:
-
Down a Group: Metallic reactivity generally increases down a group.
- Explanation: Down a group, ionization energy decreases, atomic radius increases, and electronegativity decreases. All these factors make it easier for the metal atom to lose electrons, thus increasing its reactivity. For example, the alkali metals (Group 1) become increasingly reactive as you move down the group (Li < Na < K < Rb < Cs), reacting more vigorously with water.
-
Across a Period: Metallic reactivity generally decreases across a period.
- Explanation: Across a period, ionization energy increases, atomic radius decreases, and electronegativity increases. These trends make it harder for the metal atom to lose electrons, thus decreasing its reactivity. For example, in Period 3, sodium (Na) is a very reactive metal, while magnesium (Mg) is less reactive, and aluminum (Al) is even less so.
B. Reactivity of Non-metals
Non-metals react by gaining electrons to form negative ions (anions) or by sharing electrons to achieve a stable electron configuration. The ease with which a non-metal gains electrons determines its reactivity. Therefore, non-metallic reactivity is directly related to:
- Electronegativity: A higher electronegativity means the atom has a stronger attraction for electrons, making it more reactive in gaining electrons.
- Electron Affinity: While not a trend we explicitly discussed, electron affinity is the energy change when an atom gains an electron. More negative electron affinity values (energy is released) generally indicate a greater tendency to gain electrons and thus higher reactivity.
- Atomic Radius: Smaller atomic radii generally correspond to higher electronegativities (valence electrons are closer to the nucleus and experience a stronger pull), contributing to higher reactivity.
Trends in Non-metallic Reactivity:
-
Down a Group: Non-metallic reactivity generally decreases down a group.
- Explanation: Down a group, electronegativity generally decreases, and atomic radius increases. The valence electrons are further from the nucleus and experience more shielding, making it harder for the atom to attract additional electrons. For example, the halogens (Group 17) become less reactive as you move down the group (F > Cl > Br > I). Fluorine is the most reactive non-metal, readily reacting with almost everything.
-
Across a Period: Non-metallic reactivity generally increases across a period (up to the halogens).
- Explanation: Across a period, electronegativity generally increases, and atomic radius decreases. The increasing nuclear charge and decreasing size make it easier for the atom to attract electrons. For example, in Period 3, sulfur (S) is more reactive than phosphorus (P), and chlorine (Cl) is even more reactive. The noble gases (Group 18) are generally unreactive due to their filled valence shells.
C. Reactivity of Transition Metals
The reactivity trends for transition metals are more complex than those for main group elements due to the involvement of d electrons and the possibility of multiple oxidation states. However, some general observations can be made:
- Reactivity tends to decrease across a period as ionization energy generally increases and atomic radius decreases.
- Reactivity can vary within a group, and there isn't a single, straightforward trend like in the main group elements. Factors like the stability of different oxidation states play a significant role.
Summary Table Relating Reactivity to Other Trends:
| Element Type | Reactivity Trend Down a Group | Reactivity Trend Across a Period | Related Periodic Trends | Explanation of Reactivity |
|---|---|---|---|---|
| Metals | Increases | Decreases | Decreasing IE, Decreasing EN, Increasing Atomic Radius | Easier to lose electrons due to weaker hold on valence electrons. |
| Non-metals | Decreases | Increases (up to halogens) | Decreasing EN, Increasing Atomic Radius | Easier to gain electrons due to stronger attraction for valence electrons and smaller atomic size. |
In Essence:
- Most reactive metals: Located in the lower left of the periodic table (e.g., Cs, Fr). They have low ionization energies and readily lose electrons.
- Most reactive non-metals: Located in the upper right of the periodic table (excluding noble gases) (e.g., F). They have high electronegativities and readily gain electrons.
- Least reactive elements: The noble gases (Group 18) have filled valence shells and are very stable, hence their low reactivity.
Understanding how reactivity relates to other periodic trends provides a powerful framework for predicting and explaining the chemical behavior of elements. It highlights the fundamental role of electron configuration and the forces within atoms in determining chemical interactions.
Advanced Topics
Quantum Mechanics and Electron Configurations
Quantum mechanics provides the fundamental framework for understanding the behavior of atoms and molecules, particularly the arrangement of electrons within them. This arrangement, known as the electron configuration, directly dictates an atom’s chemical properties and is intricately linked to the structure of the periodic table.
Key Quantum Mechanical Principles Governing Electron Configurations:
Several core principles from quantum mechanics underpin our understanding of electron configurations:
-
Wave-Particle Duality: Electrons exhibit both wave-like and particle-like properties. Their behavior is described by wave functions, denoted by the Greek letter ψ. These wave functions are solutions to the Schrödinger equation, a central equation in quantum mechanics.
-
Quantization of Energy: Electrons in atoms can only exist in specific energy levels, often referred to as shells. These energy levels are quantized, meaning they can only take on discrete values.
-
Atomic Orbitals: Instead of well-defined orbits as in the Bohr model, electrons reside in atomic orbitals. An atomic orbital is a region of space around the nucleus where there is a high probability of finding an electron. These orbitals are described by a set of quantum numbers:
- Principal Quantum Number (n): Determines the energy level of the electron (n = 1, 2, 3, …). Higher values of n correspond to higher energy levels and greater average distance from the nucleus.
- Angular Momentum or Azimuthal Quantum Number (l): Determines the shape of the orbital and has values from 0 to n-1. l = 0 corresponds to an s orbital (spherical), l = 1 to a p orbital (dumbbell-shaped), l = 2 to a d orbital (more complex shape), and l = 3 to an f orbital (even more complex shape).
- Magnetic Quantum Number (ml): Determines the orientation of the orbital in space. It can take integer values from -l to +l, including 0. For example, a p subshell (l=1) has three p orbitals with ml values of -1, 0, and 1, oriented along the x, y, and z axes, respectively.
- Spin Quantum Number (ms): Describes the intrinsic angular momentum of an electron, which is also quantized and referred to as spin. Electrons behave as if they are spinning, creating a magnetic dipole moment. ms can have two values: +1/2 (spin up) and -1/2 (spin down).
-
Pauli Exclusion Principle: No two electrons in an atom can have the same set of four quantum numbers. This principle limits the number of electrons that can occupy a given atomic orbital to a maximum of two, with opposite spins.
-
Hund’s Rule: When filling degenerate orbitals (orbitals with the same energy), electrons will individually occupy each orbital before pairing up in the same orbital. This minimizes electron-electron repulsion and results in a lower energy state.
-
Aufbau Principle (Building-Up Principle): Electrons generally fill atomic orbitals in order of increasing energy. The approximate energy order of orbitals is: 1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s < 4f < 5d < 6p < 7s < 5f < 6d < 7p. However, there are some exceptions to this rule due to subtle energy differences and electron-electron interactions.
The Overlap Integral and Bonding:
The concept of electron configuration is also crucial in understanding how atoms form chemical bonds. The overlap integral, mathematically represented as:
S = ∫ψA*ψBdτ
plays a significant role in determining the strength and nature of chemical bonds. Let’s break down this equation:
- ψA and ψB: These represent the atomic wave functions of two different atoms, A and B, respectively. These wave functions describe the behavior of the electrons in their respective atomic orbitals.
- ψA*: This is the complex conjugate of the wave function ψA. For real wave functions, ψA* = ψA.
- dτ: This represents an infinitesimally small volume element in three-dimensional space.
- ∫: This is the integral sign, indicating that we are summing the product of the wave functions over all space.
- S: This is the overlap integral, a dimensionless quantity.
Interpretation of the Overlap Integral:
The value of the overlap integral (S) provides a measure of the extent to which the atomic orbitals of two atoms overlap in space.
- Large Positive S: Indicates significant overlap of the wave functions in a region of space where both have the same sign (phase). This leads to constructive interference of the electron waves, resulting in increased electron density between the nuclei and the formation of a stable bonding interaction (e.g., in covalent bonds).
- Small S: Indicates minimal overlap.
- Large Negative S: Indicates significant overlap but with opposite signs (phases) of the wave functions. This leads to destructive interference and a decrease in electron density between the nuclei, resulting in an antibonding interaction.
- S = 0 (Orthogonal): Indicates no overlap between the orbitals.
Relationship to the Periodic Table’s Structure:
The structure of the periodic table is a direct consequence of the quantum mechanical principles governing electron configurations.
- Periods: The rows of the periodic table correspond to the principal quantum number (n). As you move down a period, the outermost electrons occupy orbitals with a higher principal quantum number, meaning they are in higher energy levels and further from the nucleus.
- Groups (Columns): The columns of the periodic table group elements with similar valence electron configurations. Valence electrons are the electrons in the outermost occupied shell and are primarily responsible for the chemical properties of an element. Elements in the same group tend to exhibit similar chemical behavior because they have the same number of valence electrons in similar types of orbitals.
- Blocks: The periodic table can be divided into
blocks based on the type of subshell being filled by the outermost
electrons:
- s-block (Groups 1 and 2): The outermost electrons occupy s orbitals.
- p-block (Groups 13-18): The outermost electrons occupy p orbitals.
- d-block (Transition Metals, Groups 3-12): The outermost electrons occupy d orbitals.
- f-block (Lanthanides and Actinides): The outermost electrons occupy f orbitals.
Examples:
- Hydrogen (H, Z=1): Electron configuration: 1s1. It’s in period 1 and group 1 (s-block).
- Oxygen (O, Z=8): Electron configuration: 1s2 2s2 2p4. It’s in period 2 and group 16 (p-block).
- Iron (Fe, Z=26): Electron configuration: 1s2 2s2 2p6 3s2 3p6 4s2 3d6. It’s in period 4 and group 8 (d-block).
Conclusion:
Quantum mechanics provides the theoretical foundation for understanding the arrangement of electrons in atoms. The principles of quantization, atomic orbitals, the Pauli exclusion principle, Hund’s rule, and the Aufbau principle dictate how electrons fill these orbitals, resulting in specific electron configurations for each element. The overlap integral further explains how these electron configurations lead to the formation of chemical bonds. The periodic table’s structure is a powerful visual representation of these quantum mechanical principles, organizing elements based on their electron configurations and highlighting the recurring patterns in their chemical properties. Understanding the connection between quantum mechanics and electron configurations is fundamental to comprehending the behavior of matter at the atomic and molecular level.
Anomalies in Periodic Trends
While the periodic table exhibits beautiful and predictable trends in properties like atomic radius, ionization energy, electron affinity, and electronegativity, these trends are not always perfectly linear. Understanding the anomalies or irregularities in these trends is crucial for a deeper understanding of atomic structure and behavior. These deviations often arise due to subtle interplay of quantum mechanical principles, electron-electron interactions, and effective nuclear charge.
Here’s a breakdown of common anomalies and their underlying reasons:
1. Ionization Energy Anomalies:
- General Trend: Generally increases across a period and decreases down a group.
- Anomalies:
- Dip between Group 2 (Alkaline Earth Metals) and Group 13
(Boron Group): For example, the first ionization energy of
Boron (B) is lower than Beryllium (Be).
- Reason: Removing an electron from Boron involves removing a p electron, which is higher in energy and further from the nucleus (due to some shielding by the s electrons) compared to removing an s electron from the filled 2s subshell of Beryllium. This makes it easier to ionize Boron.
- Dip between Group 15 (Nitrogen Group) and Group 16 (Oxygen
Group): For example, the first ionization energy of Oxygen (O)
is lower than Nitrogen (N).
- Reason: Nitrogen has a half-filled p subshell (2p3). The electrons in this configuration experience exchange energy, a quantum mechanical phenomenon that stabilizes the half-filled subshell. Removing an electron disrupts this stability, requiring more energy. Oxygen, with a 2p4 configuration, has one paired electron in its p orbitals. Removing one of these paired electrons reduces electron-electron repulsion, making it slightly easier than removing an electron from the stable half-filled subshell of Nitrogen.
- Dip between Group 2 (Alkaline Earth Metals) and Group 13
(Boron Group): For example, the first ionization energy of
Boron (B) is lower than Beryllium (Be).
2. Electron Affinity Anomalies:
- General Trend: Generally becomes more negative (more exothermic) across a period (excluding noble gases) and less clear down a group.
- Anomalies:
- Group 2 Elements (Alkaline Earth Metals) often have positive
or very low negative electron affinities: For example,
Beryllium (Be) and Magnesium (Mg).
- Reason: These elements have filled s subshells (ns2). Adding another electron would require placing it in a higher energy p subshell, which is energetically unfavorable.
- Noble Gases have positive electron affinities:
- Reason: Noble gases have completely filled valence shells. Adding an electron would require placing it in a much higher energy level, making the process highly endothermic.
- Nitrogen having a lower (less negative) electron affinity
than Carbon:
- Reason: Nitrogen has a half-filled p subshell (2p3). Adding another electron would require pairing it in one of the p orbitals, leading to increased electron-electron repulsion and making the process less favorable than adding an electron to Carbon’s partially filled p subshell.
- Fluorine having a lower (less negative) electron affinity
than Chlorine:
- Reason: While generally electron affinity becomes less negative down a group, Fluorine is an exception. The small size of the fluorine atom leads to significant electron-electron repulsion in its already crowded 2p subshell. When an additional electron is added, this repulsion counteracts the attraction of the nucleus, making the electron affinity less exothermic than that of the larger chlorine atom, where the added electron experiences less repulsion in the 3p subshell.
- Group 2 Elements (Alkaline Earth Metals) often have positive
or very low negative electron affinities: For example,
Beryllium (Be) and Magnesium (Mg).
3. Atomic Radius Anomalies:
- General Trend: Generally decreases across a period and increases down a group.
- Anomalies:
- Transition Metal Contraction: The atomic radii of
the transition metals do not decrease as sharply across a period as the
main group elements. Furthermore, the atomic radii of the 4d and 5d
transition metals in the same group are surprisingly similar, especially
after Lanthanum.
- Reason: The filling of the inner (n-1)d orbitals in transition metals leads to increased shielding of the outer s electrons from the full nuclear charge. This effect partially counteracts the increasing nuclear charge across the period, resulting in a less dramatic decrease in atomic radius.
- Lanthanide Contraction: The atomic radii of the
elements immediately following the lanthanides are smaller than
expected.
- Reason: The filling of the 4f orbitals in the lanthanides leads to a poor shielding effect. The f orbitals have a diffuse shape and are less effective at shielding the outer electrons from the increasing nuclear charge. This results in a stronger effective nuclear charge experienced by the outer electrons, pulling them closer to the nucleus and leading to a smaller than expected atomic radius for the elements following the lanthanides. This effect persists into the 5d transition metals, explaining the similarity in size between the 4d and 5d elements in the same group.
- Transition Metal Contraction: The atomic radii of
the transition metals do not decrease as sharply across a period as the
main group elements. Furthermore, the atomic radii of the 4d and 5d
transition metals in the same group are surprisingly similar, especially
after Lanthanum.
4. Electronegativity Anomalies:
- General Trend: Generally increases across a period and decreases down a group.
- Anomalies: Anomalies in electronegativity are less
pronounced than in ionization energy or electron affinity, but they
exist.
- The trends within the heavier p-block elements can be less consistent. Factors like relativistic effects and the increasing influence of core electrons can subtly alter electronegativity values.
- The similar electronegativities of elements exhibiting the “diagonal relationship” (e.g., Lithium and Magnesium, Beryllium and Aluminum) can be considered an anomaly compared to the simple group trend. This arises from a balance of increasing nuclear charge and increasing atomic radius as you move diagonally down and to the right.
Underlying Reasons and Quantum Mechanics:
These anomalies are fundamentally rooted in the quantum mechanical description of electrons in atoms:
- Effective Nuclear Charge (Zeff): The actual positive charge experienced by a valence electron. It’s less than the actual nuclear charge (Z) due to the shielding effect of inner electrons. Anomalies often arise when the shielding effect is not uniform or predictable.
- Shielding Effect: Inner electrons “shield” outer electrons from the full positive charge of the nucleus. The effectiveness of shielding depends on the type of orbital. s electrons are more effective at shielding than p electrons, which are more effective than d electrons, and so on. This difference contributes to ionization energy anomalies.
- Subshell Stability: Half-filled and fully-filled subshells (p3, p6, d5, d10) have extra stability due to exchange energy (a consequence of the indistinguishability of electrons and the Pauli Exclusion Principle). This stability influences ionization energies and electron affinities.
- Electron-Electron Repulsion: Electrons repel each other. When electrons are paired in the same orbital, the increased repulsion can make it easier to remove one of them (affecting ionization energy) or less favorable to add another (affecting electron affinity).
- Relativistic Effects: For very heavy elements, the electrons in the inner orbitals move at speeds approaching the speed of light. This leads to an increase in their mass and a contraction of their orbitals, which in turn affects the shielding of outer electrons and can influence properties like ionization energy and electronegativity. This is particularly important for the heavier transition metals and accounts for some of the unexpected properties in that region of the periodic table.
Illustrative Example: The Ionization Energy Anomaly between Nitrogen and Oxygen
Consider Nitrogen (N, 1s22s22p3) and Oxygen (O, 1s22s22p4).
- Nitrogen: Has a half-filled 2p subshell (px1py1pz1). Removing an electron disrupts this stable configuration.
- Oxygen: Has one paired electron in its 2p subshell (px2py1pz1). Removing one of these paired electrons reduces electron-electron repulsion, making it slightly easier than removing an electron from Nitrogen’s stable half-filled subshell.
This difference in electron configuration and the associated subshell stability explain why Oxygen has a lower first ionization energy than Nitrogen, despite being further to the right in the period (which would generally suggest a higher ionization energy).
Conclusion:
Understanding the anomalies in periodic trends requires going beyond simple generalizations and delving into the quantum mechanical factors that govern electron behavior in atoms. These irregularities are not exceptions to the rules, but rather a consequence of the complex interplay of forces and energy considerations at the atomic level. Recognizing and explaining these anomalies provides a more complete and nuanced understanding of the periodic table and the chemical behavior of the elements.
Advanced Bonding Theories: Molecular Orbital Theory and the Role of the Periodic Table
While simpler bonding theories like Lewis structures and Valence Bond Theory (VBT) provide useful frameworks for understanding chemical bonds, they have limitations in explaining certain phenomena such as the paramagnetism of oxygen or the delocalization of electrons in molecules like benzene. Molecular Orbital (MO) theory offers a more sophisticated and accurate description of chemical bonding by applying quantum mechanics to the entire molecule, rather than individual atoms.
Molecular Orbital Theory: A Quantum Mechanical Approach
At its core, MO theory states that when atoms combine to form a molecule, their atomic orbitals (AOs) combine to form molecular orbitals (MOs). Electrons in a molecule are not confined to individual atomic orbitals but are delocalized and occupy these molecular orbitals, which extend over the entire molecule.
Key Principles of MO Theory:
-
Linear Combination of Atomic Orbitals (LCAO): Molecular orbitals are formed by the linear combination of atomic orbitals of the constituent atoms. This combination can be either:
- Constructive Interference (Addition): When atomic orbitals combine in phase, they reinforce each other, leading to a bonding molecular orbital. This orbital has lower energy than the original atomic orbitals, and electron density is concentrated between the nuclei, promoting bonding.
- Destructive Interference (Subtraction): When atomic orbitals combine out of phase, they cancel each other out in the region between the nuclei, leading to an antibonding molecular orbital. This orbital has higher energy than the original atomic orbitals, and there is a node (region of zero electron density) between the nuclei, destabilizing the bond.
-
Types of Molecular Orbitals: Similar to atomic orbitals, molecular orbitals have characteristic shapes and symmetries:
- Sigma (σ) Orbitals: These are formed by the head-on overlap of atomic orbitals (s-s, s-p, p-p along the internuclear axis). They have electron density concentrated along the internuclear axis.
- Pi (π) Orbitals: These are formed by the sideways overlap of atomic orbitals (p-p). They have electron density above and below the internuclear axis.
- Delta (δ) Orbitals: Formed by the face-to-face overlap of d orbitals (less common in simple molecules).
-
Energy Level Diagrams (Molecular Orbital Diagrams): These diagrams illustrate the relative energies of the atomic and molecular orbitals.
- Bonding MOs are lower in energy than the constituent AOs.
- Antibonding MOs are higher in energy than the constituent AOs.
- Non-bonding MOs (if present) have approximately the same energy as the original atomic orbitals and do not significantly contribute to bonding.
-
Filling Molecular Orbitals: Molecular orbitals are filled with electrons according to the same rules that govern the filling of atomic orbitals:
- Aufbau Principle: Electrons fill the lowest energy MOs first.
- Hund’s Rule: When filling degenerate MOs (orbitals with the same energy), electrons will individually occupy each orbital before pairing up.
- Pauli Exclusion Principle: Each MO can hold a maximum of two electrons with opposite spins.
-
Bond Order: A measure of the net bonding interactions in a molecule, calculated as:
Bond Order = (Number of electrons in bonding MOs - Number of electrons in antibonding MOs)
A higher bond order generally indicates a stronger and shorter bond. A bond order of zero indicates that the molecule is unstable and unlikely to exist.
The Role of the Periodic Table in Molecular Orbital Theory:
The periodic table plays a crucial role in determining the nature and properties of molecular orbitals:
-
Atomic Orbitals Available for Bonding: The position of an element in the periodic table dictates the types and number of atomic orbitals available for forming molecular orbitals.
- Elements in the first and second periods primarily use s and p orbitals for bonding.
- Transition metals can utilize d orbitals in bonding.
-
Number of Valence Electrons: The group number of an element determines the number of valence electrons it contributes to the formation of molecular orbitals. This is essential for correctly populating the MO diagram.
-
Electronegativity and Energy Levels: The electronegativity of atoms influences the relative energy levels of their atomic orbitals.
- In homonuclear diatomic molecules (e.g., N₂, O₂), the atomic orbitals of the two atoms have the same energy.
- In heteronuclear diatomic molecules (e.g., CO, HF), the more electronegative atom has lower energy atomic orbitals. This asymmetry affects the energy levels and electron distribution in the molecular orbitals, leading to polar covalent bonds where electron density is shifted towards the more electronegative atom.
-
Symmetry Considerations: The symmetry of atomic orbitals and the resulting molecular orbitals is crucial for their interaction. Only atomic orbitals with the appropriate symmetry can combine effectively to form molecular orbitals. The shape of the periodic table reflects the filling of these atomic orbitals and thus influences the possible symmetries of MOs.
-
Predicting Molecular Properties: By understanding the electronic configuration of the molecule in terms of its filled molecular orbitals, MO theory can predict various properties:
- Bond strength and length: Related to bond order.
- Magnetic properties:
- Paramagnetic: Molecules with unpaired electrons in their MOs are attracted to a magnetic field (e.g., O₂).
- Diamagnetic: Molecules with all paired electrons in their MOs are weakly repelled by a magnetic field (e.g., N₂).
- Ionization energy: The energy required to remove an electron from the highest occupied molecular orbital (HOMO).
- Electron affinity: The energy change when an electron is added to the lowest unoccupied molecular orbital (LUMO).
Illustrative Examples:
- Diatomic Nitrogen (N₂):
- Nitrogen (N) has the electron configuration 1s22s22p3.
- The MO diagram for N₂ shows the combination of 2s and 2p atomic orbitals to form σ2s, σ2s*, π2p, and σ2p molecular orbitals (with π2p being lower in energy than σ2p for second-period diatomics before O₂).
- The 10 valence electrons fill the bonding MOs (σ2s², σ2s*², π2p⁴, σ2p²).
- Bond order = ½ (8 - 2) = 3 (triple bond).
- N₂ is diamagnetic (all electrons paired).
- Diatomic Oxygen (O₂):
- Oxygen (O) has the electron configuration 1s22s22p4.
- The MO diagram for O₂ is similar to N₂, but the order of π2p and σ2p is reversed due to increased nuclear charge.
- The 12 valence electrons fill the bonding MOs and partially fill the antibonding π2p* orbitals (σ2s², σ2s², σ2p², π2p⁴, π2p²).
- Bond order = ½ (8 - 4) = 2 (double bond).
- O₂ is paramagnetic (two unpaired electrons in the π2p* orbitals), which cannot be explained by simple Lewis structures.
- Carbon Monoxide (CO):
- Carbon (less electronegative) has higher energy atomic orbitals than Oxygen (more electronegative).
- The MO diagram is asymmetric, with bonding MOs having more character from oxygen AOs and antibonding MOs having more character from carbon AOs.
- The filling of MOs results in a triple bond and a slightly polar molecule with the electron density shifted towards oxygen.
Beyond Diatomic Molecules:
MO theory can be extended to polyatomic molecules. While the diagrams become more complex, the fundamental principles remain the same. Concepts like delocalized π systems in molecules like benzene are readily explained by MO theory, where the p orbitals of the carbon atoms combine to form delocalized π molecular orbitals spanning the entire ring.
Limitations of MO Theory:
While powerful, MO theory also has limitations:
- Complexity for large molecules: Constructing accurate MO diagrams for very large molecules can be computationally demanding.
- Electron correlation: The simple MO theory often treats electron-electron interactions in an average way and does not fully account for instantaneous electron correlation.
Conclusion:
Molecular orbital theory provides a powerful and accurate quantum mechanical description of chemical bonding. The periodic table serves as a crucial foundation for applying MO theory, dictating the types and energies of atomic orbitals available for bonding, the number of valence electrons, and influencing the symmetry and energy levels of the resulting molecular orbitals. Understanding the interplay between MO theory and the periodic table is essential for comprehending the electronic structure, bonding, and properties of molecules. The ability of MO theory to explain phenomena like paramagnetism and delocalized bonding highlights its superiority over simpler bonding models in providing a more complete picture of chemical bonding.
About the author
Written by Noah Kleij, PhD
Noah Kleij holds a Doctorate in Organic and General Chemistry from the prestigious University of Manchester, United Kingdom. With a deep passion for chemical sciences, Noah has contributed significantly to advancing knowledge in both organic synthesis and general chemistry principles. Their research encompasses cutting-edge methodologies and innovative problem-solving approaches.
In addition to their academic achievements, Noah is an accomplished author and educator, committed to sharing complex chemical concepts in accessible and engaging ways. Their work not only bridges theoretical and practical chemistry but also inspires the next generation of chemists to explore the field's transformative potential.